Question

An office employs thirty people speaking at least one of the languages Sanskrit, Hindi, or English. Five of them speak Sanskrit, Hindi, English. Nine speak Sanskrit and English. Twenty speak Hindi of which 12 also speak Sanskrit. Eighteen speak English, no one speaks Sanskrit. An employee selected at random is known to speak either Hindi or English, the probability that employee speak only two of three languages is
(a) $\dfrac{14}{15}$
(b) $\dfrac{7}{15}$
(c) $\dfrac{1}{6}$
(d) $\dfrac{5}{6}$

Answer 1

Hint : In order to solve this problem, we need to draw the Venn diagram and find all the values of the Venn diagram. The formulas that we will encounter while solving this are as follows, $n\left( H\cup S\cup E \right)=n\left( S \right)+n\left( H \right)+n\left( E \right)-n\left( H\cap E \right)-n\left( H\cap S \right)-n\left( E\cap S \right)+n\left( H\cap S\cap E \right)$
Where $\cup$ shows the union of two sets and $\cap$ shows the intersection of two events.

Complete step-by-step answer :
We can solve this problem using the Venn diagram.
Let the event of speaking English be E.
Let the event of speaking Sanskrit be S.
Let the event of speaking Hindi be H.
Hence, the number of people speaking English are $n\left( E \right)$ .
The number of people speaking Sanskrit are $n\left( S \right)$ .
The number of people speaking Hindi are $n\left( H \right)$ .
We can show this in the venn diagram as follows,

According to the condition, we are given that the five people speak Sanskrit, Hindi and English so the region of intersection of all three circles is 5.
It can be represented as $n\left( S\cap H\cap E \right)=5$ .
9 people speak Sanskrit and English.
Therefore, $n\left( S\cap E \right)=9$ .
20 people speak Hindi and 12 speak Hindi and Sanskrit.
$\begin{aligned} & n\left( H \right)=20 \\\ & n\left( H\cap S \right)=12 \\\ \end{aligned}$
18 people speak English.
$n\left( E \right)=18$
Zero people only speak Sanskrit.
Therefore, we can say that $n\left( S \right)$ consists of people who also speak Hindi, English or both.
Therefore, we can write the equation
$n\left( S \right)=n\left( S\cap E \right)+n\left( S\cap H \right)-n\left( S\cap E\cap H \right)$
Substituting we get,
$n\left( S \right)=9+12-5=16$
We need to find the value of $n\left( H\cap E \right)$ .
The formula says that $n\left( H\cup S\cup E \right)=n\left( S \right)+n\left( H \right)+n\left( E \right)-n\left( H\cap E \right)-n\left( H\cap S \right)-n\left( E\cap S \right)+n\left( H\cap S\cap E \right)$
Substituting all the values we get,
$30=16+20+18-n\left( H\cap E \right)-12-9+5$
Therefore, solving for $n\left( H\cap E \right)$ , we get,
$n\left( H\cap E \right)=16+20+18-30-12-9+5=8$
We can show all the values in the Venn diagram.

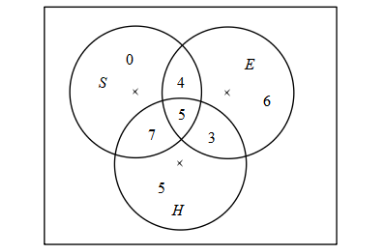
As we can see that in $n\left( S\cap E \right)=9$ but while filling the values we filled the region with only Sanskrit and English is 4 because 5 people speak all the 3 languages.
We need to follow the same procedure and satisfy all the conditions.
Now we are given the final condition that the person speaks either English or Hindi.
By counting from the Venn diagram we can say that there are in total 30 people who speak English or Hindi language.
We need to find the probability for the event where the person speaks only two languages.
The people speaking only English and Sanskrit are 4.
The people speaking only English and Hindi are 3.
The people speaking Sanskrit or Hindi are 7.
The total number of people speaking any two languages are 3 + 4 + 7 = 14.
Therefore, the probability is given by the formula as follows,
$\text{Probability = }\dfrac{\text{Event}}{\text{Total possible of comes}}$
Substituting we get,
Probability = $\dfrac{14}{30}=\dfrac{7}{15}$ .
So, the correct answer is “Option B”.

Note : We need to understand that in $n\left( S\cap E \right)=9$ but while filling the values we filled the region with only Sanskrit and English is 4 because 5 people speak all the 3 languages.
Similarly in $n\left( S\cap H \right)=12$ but while filling the values we filled the region with only Sanskrit and English is 7, because 5 people speak 5 people all the 4 languages.