Question

An observer $1.5$ meters tall is $20.5$ meters away from a tower $22$ meters high. Determine the angle of elevation of the tower from the eye of the observer?
a)${60^ \circ }$
b)${45^ \circ }$
c)${30^ \circ }$
d)${75^ \circ }$ $$$$

Answer 1

Hint : We know trigonometric formulas like of $\cos \theta = \dfrac{{base}}{{{\text{Hypotenuse}}}}$ , $\sin \theta = \dfrac{{perpendicular}}{{{\text{Hypotenuse}}}}$ , $\tan \theta = \dfrac{{perpendicular}}{{base}}$ .And values of, $\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }}$ , $\tan {45^ \circ } = 1$ , $\tan {60^ \circ } = \sqrt 3$ . The angle of elevation is the angle formed by the horizontal line of sight and the object when a person stands and looks up at it. The distance between the head and eye of a boy should be neglected.

Complete step-by-step answer :
We should know angle of elevation and angle of depression that is
The angle of elevation is the angle formed by the horizontal line of sight and the object when a person stands and looks up at it.
we should try to draw its diagrams,
And diagram for the following question is:

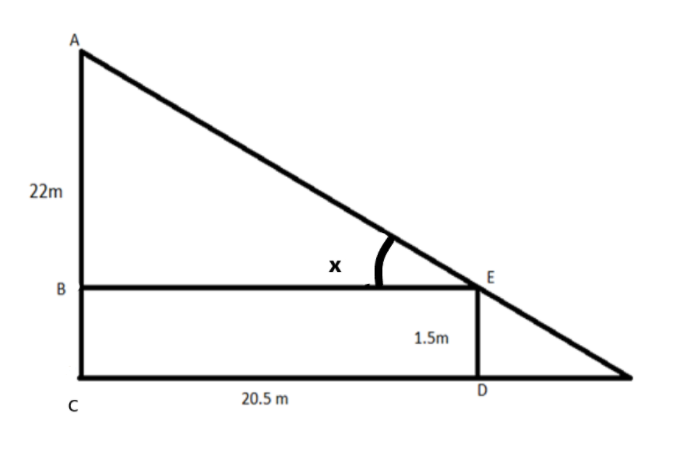
We have labelled diagram as:
Total height of pole is labelled as AC = height of pole
Height of boy is labelled as ED= height of boy
Distance between the boy and pole CD=distance between boy and pole
As line BE is parallel to CD and we know that distance between two parallel lines are always equal
Since $ED{\text{ }} = 1.5$, so$BC = 1.5$
For calculating the length of AB
AB=AC-BC
$AB = 22 - 1.5$
$AB = 20.5$
From diagram, CD=BE
BE=20.5
And we know that $\tan \theta = \dfrac{{perpendicular}}{{base}}$
In triangle ABE
$\tan x = \dfrac{{AB}}{{BE}}$
$\tan x = \dfrac{{20.5}}{{20.5}}$
$\tan x = 1$
And we know that $\tan {45^ \circ } = 1$
So, angle of elevation is ${45^ \circ }$
So, the correct answer is “Option B”.

Note : The angle of elevation is the angle formed by the horizontal line of sight and the object when a person stands and looks up at it. The angle of depression is the angle between the horizontal line of sight and the object when a person stands and stares down at an item. If the problem that is to be solved is a right-angled triangle with an angle and a side known, trigonometric ratios can be used to find the remaining angles and sides.