Question

An oblique projectile projected from the ground takes time $4s$ to travel from $P$ to $Q$ while takes $2s$ to travel from $S$ to $T$. The height $h$ of level $ST$ from level $PQ$ is:

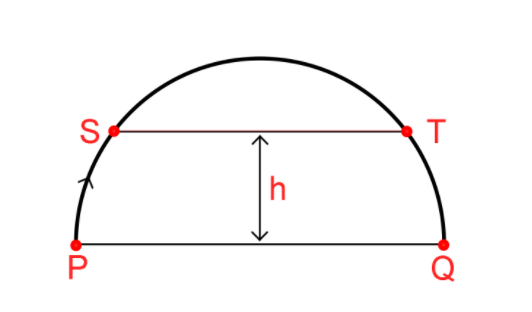
(A). $15m$
(B). $10m$
(C). $12.5m$
(D). $8.5m$

Answer 1

You can start by explaining projectiles. Then write the equation for the time of flight of a projectile and the equation for the maximum height i.e. $t = \dfrac{{2u\sin \theta }}{g}$ for the motion of projectile from point $P$ to $Q$ and from $S$ to $T$ and calculate the value of $u\sin \theta$ and $u'\sin \theta$. Then use the equation Maximum height $= \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}$ and calculate the maximum height for the motion of projectile from point $P$ to $Q$ and from $S$ to $T$. Then find the difference between these two to reach the solution.

Complete step-by-step answer :
Projectiles are bodies that are launched with some initial velocity, reach a certain maximum height while covering a certain horizontal range. An example of projectiles is a ball thrown into the sky.

Given time of flight of a projectile for motion from point $P$ to $Q = 4\sec$ and for the motion from point $S$ to $T = 2\sec$ .
Let’s assume that the velocity of the projectile at the point $P$ is $u$ and the velocity of the projectile at the point $S$ is $u'$ .
We know that the equation for the time of flight of a projectile is
$t = \dfrac{{2u\sin \theta }}{g}$
So, for the motion of the projectile from point $P$ to $Q$ , we have
$\dfrac{{2u\sin \theta }}{g} = 4\sec$
$u\sin \theta = \dfrac{{4g}}{2} = 2g$
$u\sin \theta = 20m/s$ (Taking $g = 10m/{s^2}$ )
And, for the motion of the projectile from point $S$ to $T$ , we have
$\dfrac{{2u'\sin \theta }}{g} = 2$
$\Rightarrow u'\sin \theta = g = 10m/s$
We also know that the equation for the maximum height is
Maximum height $= \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}$
So, the maximum height for the motion of the projectile from point $P$ to $Q$ is
$H = \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}} = \dfrac{{400}}{{2 \times 10}}$
$\Rightarrow H = 20m$
And, the maximum height for the motion of the projectile from point $S$ to $T$ is
$H' = \dfrac{{u{'^2}{{\sin }^2}\theta }}{{2g}} = \dfrac{{100}}{{2 \times 10}} = 5m$
$\therefore h = H - H' = 15m$
Hence, option A is the correct choice.

Note : In the solution above, we have used the equations for the time of flight of projectile and the maximum height of the projectile, i.e. $t = \dfrac{{2u\sin \theta }}{g}$ and Maximum height $= \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}$ respectively. We could also use the equations for motion, but it would be an unnecessarily long method.