Question

An object weighs $10N$ at the north pole of the earth. In a geostationary satellite distance $7R$ from the center of the earth (of radius R), the true weight and the apparent weight are.
A. $0N,0N$
B. $0.2N,0N$
C. $0.2N,9.8N$
D. $0.2N,0.2N$

Answer 1

The weight of any object depends on the acceleration due to gravity acting on the body and the mass of the body. The mass is a constant quantity but the value of g (acceleration due to gravity) changes according to the gravitational force acting on the body. As the object moves away from the surface of the earth.

Formula used: As per the given data,
The weight of the body at the north pole $10N$
Radius of earth $R$
The distance of the object (starlight) from the center of the earth is $7R$.
Formula to be used,
Weight ($W$) is given by $w=mg$
$g'=g{{\left( \dfrac{R}{R+h} \right)}^{2}}$
Where $g'$ is the acceleration due to gravity acting on the object at a certain height.

Complete step by step answer:
According to the question, starlight is situated (north pole) at a height of $7R$ from the center of the earth with radius $R$. This can be visualized with the diagram given below,

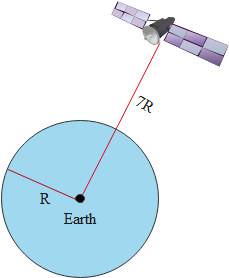
As per the situation given in the question weight of the body is $10N$. But as we know that the weight of the body at a certain distance from the center of the earth is given as,
$W=mg'$
Where,
$m$ is the mass of the starlight
$g'$ is the acceleration due to gravity acting on the object at a certain height.
The value of $g'$ is given by,
$g'=g{{\left( \dfrac{R}{R+h} \right)}^{2}}$
The distance of the object from the surface of the earth will be ($7R-R=6R$)
So by putting the known values the value of g’ will be,
$\begin{aligned} & g'=g{{\left( \dfrac{R}{7R} \right)}^{2}} \\\ & g'=\dfrac{g}{49} \\\ \end{aligned}$
So the actual weight of the object at the North pole can be written as,
$\begin{aligned} & {{W}_{ac}}=\dfrac{mg}{49} \\\ & \Rightarrow {{W}_{ac}}=\dfrac{10}{49} \\\ & \Rightarrow {{W}_{ac}}=0.2N \\\ \end{aligned}$
Let the acceleration of the satellite be $a$
As the satellite is considered free falling so the acceleration of the satellite will be the same as the acceleration due to gravity acting on the satellite. So the apparent weight of the satellite will be,
$\begin{aligned} & {{W}_{ap}}=m(g'-a) \\\ & \Rightarrow {{W}_{ap}}=m(0.2-0.2) \\\ & \Rightarrow {{W}_{ap}}=0N \\\ \end{aligned}$
So the apparent weight of the satellite will be zero.

So, the correct answer is “Option B”.

Note: The apparent and the actual weight are the two kinds of weight representation with respect to the different reference frames. The actual weight is measured with reference to the gravitational force and the object is considered to be stationary. But on the other hand the apparent weight of the actual condition of motion is also taken into account.