Question

An object shot from the bottom of a long, smooth plane inclined at an angle of $60^\circ$ with the horizontal, travels a distance ${x_1}$ along the plane. If the inclination is decreased to $30^\circ$ and the same object is shot with the same velocity, it travels a distance ${x_2}$. Find ${x_1}:{x_2}$.
A) $1:\sqrt 2$
B) $\sqrt 2 :1$
C) $1:\sqrt 3$
D) $1:2\sqrt 3$

Answer 1

Use Newton’s equation of motion that gives a relation between initial velocity $u$, final velocity $v$, acceleration $a$ and distance travelled $x$.

Complete step by step solution:
Step 1: Sketch the free body diagram of the setup to get an idea of the forces acting on the object.

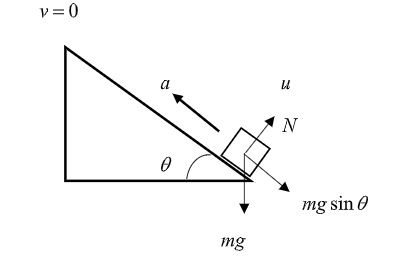
Step 2: Obtain an expression for the distance traveled using the data from the above diagram.
From the diagram, we have the acceleration of the body as $a = - g\sin \theta$ .
Newton’s equation of motion gives us, ${v^2} = {u^2} + 2ax$ .
The object is shot from the bottom of the plane, once the object covers a distance $x$, the velocity of the object becomes zero.
i.e., if initial velocity is $u$ then final velocity $v = 0$ as the object covers the distance $x$ .
Substituting the values for $v$ and $a$ in the equation of motion, we get $0 = {u^2} + 2( - g\sin \theta )x$.
Rearrange the above equation to obtain the expression for $x$.
Now, the stopping distance, $x = \dfrac{{{u^2}}}{{ - 2g\sin \theta }}$ .
Step 3: Express the relation for the stopping distance in the two cases.
Case 1: The plane is inclined at $60^\circ$ and the object is shot from the bottom of the pane.
Here the angle of inclination $\theta = 60^\circ$ and the stopping distance is denoted by ${x_1}$ .
The initial velocity is $u$ and final velocity is $v = 0$ .
Then, stopping distance ${x_1} = \dfrac{{{u^2}}}{{ - 2g\sin 60}}$ .
Case 2: The plane is inclined at $30^\circ$ and the object is shot from the bottom of the pane.
Here the angle of inclination $\theta = 30^\circ$ and the stopping distance is denoted by ${x_2}$.
The initial velocity is $u$ and final velocity is $v = 0$ .
Then, stopping distance ${x_2} = \dfrac{{{u^2}}}{{ - 2g\sin 30}}$ .
Step 4: Find the ratio ${x_1}:{x_2}$.
We have, ${x_1} = \dfrac{{{u^2}}}{{ - 2g\sin 60}}$ and ${x_2} = \dfrac{{{u^2}}}{{ - 2g\sin 30}}$ then ${x_1}:{x_2}$ is given by,
${x_1}:{x_2} = \dfrac{{\left( {\dfrac{{{u^2}}}{{ - 2g\sin 60}}} \right)}}{{\left( {\dfrac{{{u^2}}}{{ - 2g\sin 30}}} \right)}}$ .
Cancel out similar terms to obtain, $\dfrac{{{x_1}}}{{{x_2}}} = \dfrac{{\sin 30}}{{\sin 60}}$ .
Since, $\sin 30 = \dfrac{1}{2}$ and $\sin 60 = \dfrac{{\sqrt 3 }}{2}$ , we have $\dfrac{{{x_1}}}{{{x_2}}} = \dfrac{1}{{\sqrt 3 }}$ .

Therefore, the correct option is (C) $1:\sqrt 3$.

Additional information:
The solenoid is used to generate magnetic fields. This is done by allowing current to pass through it. The arrangement of two solenoids kept at some distance from each other and placed in an evacuated chamber can act as a magnetic bottle. The solenoids will act as a mirror or reflector to the approaching charged particles.

Note:
While sketching the free body diagram the weight of the body is resolved into its components. The component antiparallel to the normal force gets canceled. Stopping distance is the distance covered by the object when it is shot with initial velocity from the bottom of the plane. As the angle of inclination decreased from $60^\circ$ to $30^\circ$, the stopping distance increased. i.e., ${x_2} > {x_1}$ . Thus, the higher the inclination angle, the lesser will be the stopping distance.