Question

An object of specific gravity $\rho$ is hung from a thin steel wire. The fundamental frequency for transverse standing waves in wire is $300Hz$. The object is immersed in water so that one half of its volume is submerged. The new fundamental frequency in $Hz$ is

& \text{A}\text{. 300}{{\left( \dfrac{2\rho -1}{2\rho } \right)}^{\dfrac{1}{2}}} \\\ & \text{B}\text{. 300}{{\left( \dfrac{2\rho }{2\rho -1} \right)}^{\dfrac{1}{2}}} \\\ & \text{C}\text{. 300}\left( \dfrac{2\rho }{2\rho -1} \right) \\\ & \text{D}\text{. 300}\left( \dfrac{2\rho -1}{2\rho } \right) \\\ \end{aligned}$$

Answer 1

First calculate the frequency when the object is in air in terms of tension on the string and string length. Then calculate the frequency when the object is half in water. When the object is submerged there is an upthrust force on the object which is directly proportional to the volume submerged. So the tension on the string when the object is dipped half in water will be reduced . Then compare the two frequencies to get the answer.

Formula used:
$\begin{aligned} & Volume=\dfrac{mass}{density} \\\ & \text{For a object to be in equilibrium the tension on string must be equal to its weight} \\\ & \text{i}\text{.e}\text{. }T=mg \\\ \end{aligned}$
Frequency of the block of mass $m$of string length $l$ with tension on string $T$is given by $f=\dfrac{1}{2l}\sqrt{\dfrac{T}{m}}$
Upthrust force is given by $\begin{aligned} & {{F}_{upthrust}}=\text{density of liquid volume of liquid displaced}\times \text{acceleration due to gravity} \\\ & {{F}_{upthrust}}={{\rho }_{liquid}}\times Volume\times g \\\ \end{aligned}$

Complete step-by-step answer:

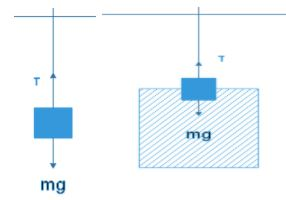
In the first case the block is suspended from a rod in the air. The block is at rest so the tension on the rod will be equal to the weight of the block.
i.e $T=mg=\rho Vg$
where $\rho =\text{ specific gravity of object ,}V=\text{volume so }m=\rho V$
So frequency in air will be
${{f}_{a}}=\dfrac{1}{2l}\sqrt{\dfrac{T}{m}}=\dfrac{1}{2l}\sqrt{\dfrac{\rho Vg}{m}}$
When the object is half immersed in water i.e. half of the volume of the object is immersed in water.
In this case Tension will be equal to
${{T}_{water}}=mg-{{F}_{upthrust}}$
Here $mg=\rho Vg$ and ${{F}_{upthrust}}={{\rho }_{water}}\dfrac{V}{2}g$ because half of the object is immersed so half of the volume of the block will displace water.
${{T}_{water}}=\rho Vg-{{\rho }_{water}}\dfrac{V}{2}g=\dfrac{Vg}{2}\left( 2\rho -{{\rho }_{water}} \right)$
So the frequency in water is
${{f}_{water}}=\dfrac{1}{2l}\sqrt{\dfrac{{{T}_{water}}}{m}}=\dfrac{1}{2l}\sqrt{\dfrac{Vg\left( 2\rho -{{\rho }_{water}} \right)}{2m}}=\dfrac{1}{2l}\sqrt{\dfrac{Vg\rho }{m}}\sqrt{\left( \dfrac{2\rho -{{\rho }_{water}}}{2\rho } \right)}$
But ${{f}_{a}}=\dfrac{1}{2l}\sqrt{\dfrac{Vg\rho }{m}}$
So ${{f}_{water}}={{f}_{a}}\sqrt{\left( \dfrac{2\rho -{{\rho }_{water}}}{2\rho } \right)}$
Given ${{f}_{a}}=300Hz$
So ${{f}_{water}}=300\sqrt{\left( \dfrac{2\rho -{{\rho }_{water}}}{2\rho } \right)}Hz$
But ${{\rho }_{water}}=1$
So ${{f}_{water}}=300\sqrt{\left( \dfrac{2\rho -1}{2\rho } \right)}Hz$

So, the correct answer is “Option A”.

Note: For problems like this calculate the resultant force on the object. And for equilibrium condition write down the equation. Also the upthrust or buoyancy force is dependent upon the volume of the displaced liquid. You can also calculate the time-period of oscillation. Just be careful for equilibrium force conditions.