Question

An object of height $6\ cm$ is placed perpendicular to the principal axis of a concave lens of focal length $5\ cm$. Use the lens formula to determine the position, size and nature of the image if the distance of the object from the lens is $10\ cm$.

Answer 1

First of all, we will find the image distance by using the relation between object distance, image distance and focal length of the lens which can be given mathematically as, $\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}$. Now, using the image distance we can find the magnification of the lens and from that we can find the size and nature of the image by using the relation, $m=\dfrac{v}{u}=\dfrac{{{h}_{1}}}{{{h}_{2}}}$.

Formula used:
$\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}$, $m=\dfrac{v}{u}=\dfrac{{{h}_{1}}}{{{h}_{2}}}$

Complete step by step answer:
In question we are given that an object of height $6\ cm$ is placed perpendicular to the principal axis of a concave lens of focal length $5\ cm$ and the distance of the object from lens is $10\ cm$ and we are asked to find the position, height and nature. Now, the diagram for that is given below,

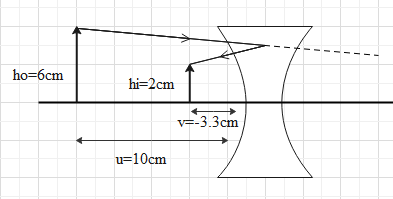
So, first of all the relation between object distance, image distance and focal length of the lens which can be given mathematically as,
$\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}$
Where, u is object distance, v is image distance and f is focal length of the lens.
In case of concave lens, the image distance and focal length are considered as negative so the values of object distance and focal length can be given as,
$u=-10\ cm$
$f=-5\ cm$
On substituting these values, we will get,
$\dfrac{1}{v}-\dfrac{1}{\left( -10 \right)}=-\dfrac{1}{5}$
$\Rightarrow \dfrac{1}{v}=-\dfrac{1}{5}-\dfrac{1}{10}$
$\Rightarrow \dfrac{1}{v}=\dfrac{-10-5}{50}$
$\Rightarrow v=-\dfrac{10}{3}=-3.33\ cm$
Now, the relation between image distance (v), object distance (u) and magnification (m) can be given by the formula,
$m=\dfrac{v}{u}=\dfrac{{{h}_{2}}}{{{h}_{1}}}$
where, ${{h}_{1}}$ is object height and ${{h}_{2}}$ is image height.
Now, the object height is $6\ cm$ as per the question, so on substituting this value in equation we will get,
$m=\dfrac{-3.33}{-10}=\dfrac{{{h}_{2}}}{6}\Rightarrow {{h}_{2}}=\dfrac{6\times 3.33}{10}$
$\Rightarrow {{h}_{2}}=2cm$
From this we can say that the image distance will be $-3.33\ cm$in front of the lens and the height of the image formed will be $2\ cm$ and it will be virtual and erect in nature.

Note:
Many a time student use the formula of concave mirror i.e. $\dfrac{1}{v}+\dfrac{1}{u}=\dfrac{1}{f}$ instead of concave lens i.e. $\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}$ and due to that the whole sum goes wrong. Students should remember that if the image is formed in front of the lens then the image distance is negative and if it Is formed at the back of the lens then the image distance will be positive because the change in sign also changes the complete answer so students must be careful regarding it.