Question

An object moving with Velocity v = (2i + 3j + 4k )

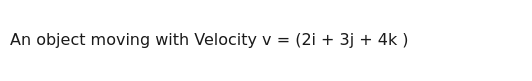
Answer 1

sqrt(29)

Answer 2

The question provides the velocity vector of an object at a certain instant. The velocity vector is given as $\vec{v} = (2\hat{i} + 3\hat{j} + 4\hat{k})$. A standard calculation performed when given a velocity vector is finding its magnitude, which represents the speed of the object.

The velocity vector is $\vec{v} = v_x \hat{i} + v_y \hat{j} + v_z \hat{k}$, where $v_x = 2$, $v_y = 3$, and $v_z = 4$. The magnitude of the velocity vector, which is the speed of the object, is given by the formula:

$|\vec{v}| = \sqrt{v_x^2 + v_y^2 + v_z^2}$

Substitute the components of the given velocity vector into the formula:

$|\vec{v}| = \sqrt{2^2 + 3^2 + 4^2}$

$|\vec{v}| = \sqrt{4 + 9 + 16}$

$|\vec{v}| = \sqrt{29}$

Thus, the speed of the object is $\sqrt{29}$.