Solveeit Logo
Login

Question

Question: An object moves towards the mirror as well as the mirror moves towards the object with the same velo...

An object moves towards the mirror as well as the mirror moves towards the object with the same velocity of 1m/s. Determine the velocity of the image with respect to ground.

Explanation

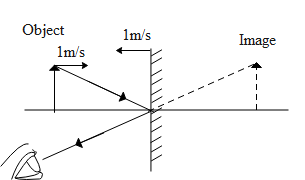
Solution

The mirror and the object moves towards each other. Hence there is a relative velocity between the object with respect to the mirror. Similarly the image will also behave in similar fashion as that of the object with respect to the mirror. Further accordingly from the relative velocity of the image with respect to the mirror we can determine its velocity with respect to ground.
Formula used:
vi/m=vi−vm{{v}_{i/m}}={{v}_{i}}-{{v}_{m}}

Complete answer:
Let us say the speed of the mirror as vm{{v}_{m}}, speed of the object as vo{{v}_{o}} and speed of the image as vi{{v}_{i}} with respect to ground. Let us say we wish to observe this situation with the perspective of the mirror. Hence the relative speed of the object with respect to the mirror i.e. vo/m{{v}_{o/m}} will be,
vo/m=vo−vm{{v}_{o/m}}={{v}_{o}}-{{v}_{m}}
Let us assume the direction of speed of the object is positive and as a result the image and the mirror velocity will be negative. Using the above equation we get,
vo/m=vo−vm ⇒vo/m=1m/s−(−1m/s) ⇒vo/m=2m/s \begin{aligned} & {{v}_{o/m}}={{v}_{o}}-{{v}_{m}} \\\ & \Rightarrow {{v}_{o/m}}=1m/s-(-1m/s) \\\ & \Rightarrow {{v}_{o/m}}=2m/s \\\ \end{aligned}
Hence with respect to the mirror the object moves with the speed of 2m/s. The plane mirror forms an image such that the object distance is always equal to the image distance with respect to the mirror. Hence its velocity with respect to the mirror is also the same but opposite in sign. Hence
vi/m=−2m/s ⇒vi/m=vi−vm ⇒−2m/s=vi−(−1ms) ⇒vi=−1ms−2m/s=−3m/s \begin{aligned} & {{v}_{i/m}}=-2m/s \\\ & \Rightarrow {{v}_{i/m}}={{v}_{i}}-{{v}_{m}} \\\ & \Rightarrow -2m/s={{v}_{i}}-(-1ms) \\\ & \Rightarrow {{v}_{i}}=-1ms-2m/s=-3m/s \\\ \end{aligned}
Therefore the speed of the image with respect to ground is -3m/s.

Note:
The negative sign indicates that the image and the object are approaching each other as the object moves towards the mirror. The relative velocity with respect to the mirror means we can treat the mirror to be at rest. And hence only consider the motion of the object and the image.