Question

An object is thrown upward with a velocity u, then the displacement-time graph is?

Answer 1

The question is based on one dimensional motion of a particle. As here an object is thrown vertically upward and we consider the one dimensional motion of the object in vertical direction. As there is gravity and it attracts the object towards the earth surface hence the velocity of the object is affected by gravity.

Complete step by step solution:
Step 1: Let us consider an object is thrown vertically upward with a velocity $u$. And after time $t$ the object reaches at height $s$. Then the one dimensional equation of motion is,
$s = ut - \dfrac{1}{2}g{t^2}$---------------------- (1) where, $g =$ gravitational constant.
Step 2: From equation (1) we can see that vertical distance $h$is a quadratic function of t.
Now, the maximum height of the object is obtained from the relation ${v^2} = {u^2} - 2gs$---- (2)
Where, $v$= the velocity of the object at height${s_{\max }}$. ${s_{\max }}$ is the maximum height of the object.
At maximum height $v = 0$that means the object stops at${s_{\max }}$.
Then from equation (2) we get $0 = {u^2} - 2g{s_{\max }}$
Or, ${u^2} = 2g{s_{\max }}$ Or, ${s_{\max }} = \dfrac{{{u^2}}}{{2g}}$
Step 3: Now if the speed of the object is $v$ at time$t$. Then we get, $v = u - gt$----- (3)
At height ${s_{\max }}$ , $v = 0$and $t = {t_{\max }}$; then from equation (3) we get $0 = u - g{t_{\max }}$
Or, ${t_{\max }} = \dfrac{u}{g}$
Therefore, time taken ${t_g}$to reach ground is twice of ${t_{\max }}$. That is ${t_g} = \dfrac{{2u}}{g}$.

Step 4: As per explanation given above the displacement – time graph is represented as

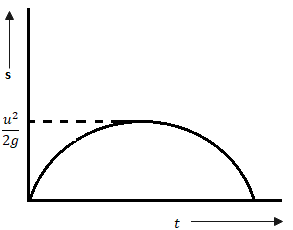
Therefore, option (A) is correct.

Note: Student has to remember the equation of one dimensional motion under the gravitational acceleration$g$. Let an object be thrown vertically upward with an initial speed$u$. And at time $t$ the velocity of the object will be $v$ and height will be $s$then three equations of motion are:
$v = u - gt$
$s = ut - \dfrac{1}{2}g{t^2}$
${v^2} = {u^2} - 2gs$.