Question

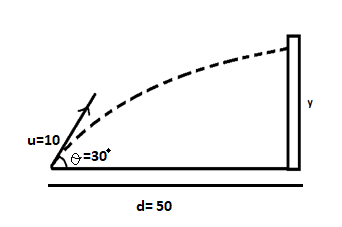
An object is thrown towards the tower which is at a horizontal distance of 50 m with an initial velocity of $10m{s^{ - 1}}$ and making an angle 30° with the horizontal. The object hits the tower at a certain height. The height from the bottom of the tower, where the object hits the tower is (Take g = $10m{s^{ - 2}}$ )
A) $\dfrac{{50}}{{\sqrt 3 }}\left[ {1 - \dfrac{{10}}{{\sqrt 3 }}} \right]m$
B) $\dfrac{{50}}{3}\left[ {1 - \dfrac{{10}}{{\sqrt 3 }}} \right]m$
C) $\dfrac{{100}}{{\sqrt 3 }}\left[ {1 - \dfrac{{10}}{{\sqrt 3 }}} \right]m$
D) $\dfrac{{100}}{3}\left[ {1 - \dfrac{{10}}{{\sqrt 3 }}} \right]m$

Answer 1

We can draw the diagram according to the question and resolve the velocity into its horizontal and vertical components. As the tower stands along the y – axis, its distance along the same axis needs to be calculated which can be done by finding unknown values from that along x – axis using the equation of motion.
$s = ut + \dfrac{1}{2}a{t^2}$

Complete step by step answer:
Given:
Initial velocity (u) = $10m{s^{ - 1}}$
Angle $\left( \theta \right)$ = 30°
Distance along x – axis (x) = 50 m
Distance along y – axis (y) = Height of tower = ?

The velocity can be resolved its horizontal and vertical components

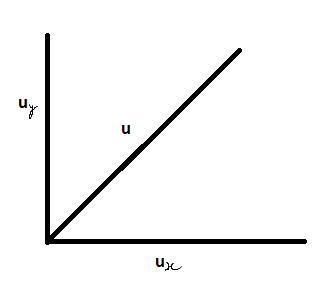
Here
${u_x} = u\cos \theta$ (as it is along x – axis) _______ (1)
${u_y} = u\sin \theta$ (as it is along y – axis) _________ (2)
We have,
u = $10m{s^{ - 1}}$
$\theta$ = 30°
Calculating the value of ${u_x}$ and ${u_y}$:
From (1),
${u_x} = u\cos \theta$
Substituting respective values:
${u_x} = 10\cos {30^ \circ }$
${u_x} = 10 \times \dfrac{{\sqrt 3 }}{2}$ $\left( {\because \cos {{30}^ \circ } = \dfrac{{\sqrt 3 }}{2}} \right)$

${u_x} = 5\sqrt 3 m{s^{ - 1}}$
Similarly, from (2),
${u_y} = u\sin \theta$
Substituting respective values:
${u_y} = 10\sin {30^ \circ }$
${u_y} = 10 \times \dfrac{1}{2}$ $\left( {\because \sin {{30}^ \circ } = \dfrac{1}{2}} \right)$
${u_y} = 5m{s^{ - 1}}$
Now,
Acceleration is only acceleration due to gravity acting in downward direction along y – axis. Therefore,
Acceleration along x – axis : ${a_x} = 0$
Acceleration along x – axis : ${a_y} = - g$
Using equation of motion:
$s = ut + \dfrac{1}{2}a{t^2}$
Where,
s = distance
t = time
u = initial velocity
a = acceleration
Applying this on the respective axis, we get:
$x = {u_x}t + \dfrac{1}{2}{a_x}{t^2}$
Substituting the values:
$50 = 5\sqrt 3 t + \dfrac{1}{2}(0){t^2}$

$$t = \dfrac{{50}}{{5\sqrt 3 }} \\\ = \dfrac{{10}}{{\sqrt 3 }}s \\\$$

Similarly
$y = {u_y}t + \dfrac{1}{2}{a_y}{t^2}$
Substituting all the values:
$y = 5 \times \dfrac{{10}}{{\sqrt 3 }} + \dfrac{1}{2}( - 10){\left( {\dfrac{{10}}{{\sqrt 3 }}} \right)^2}$

$y = 5 \times \dfrac{{10}}{{\sqrt 3 }} - 5 \times \dfrac{{10}}{{\sqrt 3 }} \times \dfrac{{10}}{{\sqrt 3 }}$
$y = \dfrac{{50}}{{\sqrt 3 }}\left( {1 - \dfrac{{10}}{{\sqrt 3 }}} \right)m$
Value of y denotes the along y – axis which is equal to the height of the tower.
Therefore, the height from the bottom of the tower, where the object hits the tower is $\dfrac{{50}}{{\sqrt 3 }}\left[ {1 - \dfrac{{10}}{{\sqrt 3 }}} \right]m$ , option A).

Note: This thrown object is a projectile in X –Y plane and hence follows the rule of projectile where there is acceleration due to gravity at all points is acting in downward direction.
When resolving, the component along x – axis is generally measured in terms of cos and along y –axis in terms of sine.