Question

An object is thrown at an angle of $\theta$ with horizontal. If the elevation angle of an object at its highest point as seen from a point of projection is ${\tan ^{ - 1}}\left( {\dfrac{1}{2}} \right)$. Then $\theta$ is equal to:
(A) $30^\circ$
(B) $45^\circ$
(C) $60^\circ$
(D) $37^\circ$

Answer 1

Hint
In the question, it is given that, if the object is observed at an inclination, this angle can be used to determine the range and height. By knowing the relation between range and height, the angle of projection can be found.
$\Rightarrow H = \dfrac{{{U^2}{{\sin }^2}\theta }}{{2g}}$
$\Rightarrow R = \dfrac{{{U^2}2\sin \theta \cos \theta }}{g}$
$\Rightarrow \tan ({\tan ^{ - 1}}x) = x$

Complete step by step answer
When the projectile is thrown, it follows a parabolic path, where it reaches a maximum height equal to-
$\Rightarrow H = \dfrac{{{U^2}{{\sin }^2}\theta }}{{2g}}$
The horizontal distance or range covered during the flight of the projectile, or range is given by-
$\Rightarrow R = \dfrac{{{U^2}2\sin \theta \cos \theta }}{g}$
Here U is the initial velocity of the object
And g is the acceleration due to gravity.
The following diagram makes the question clear-

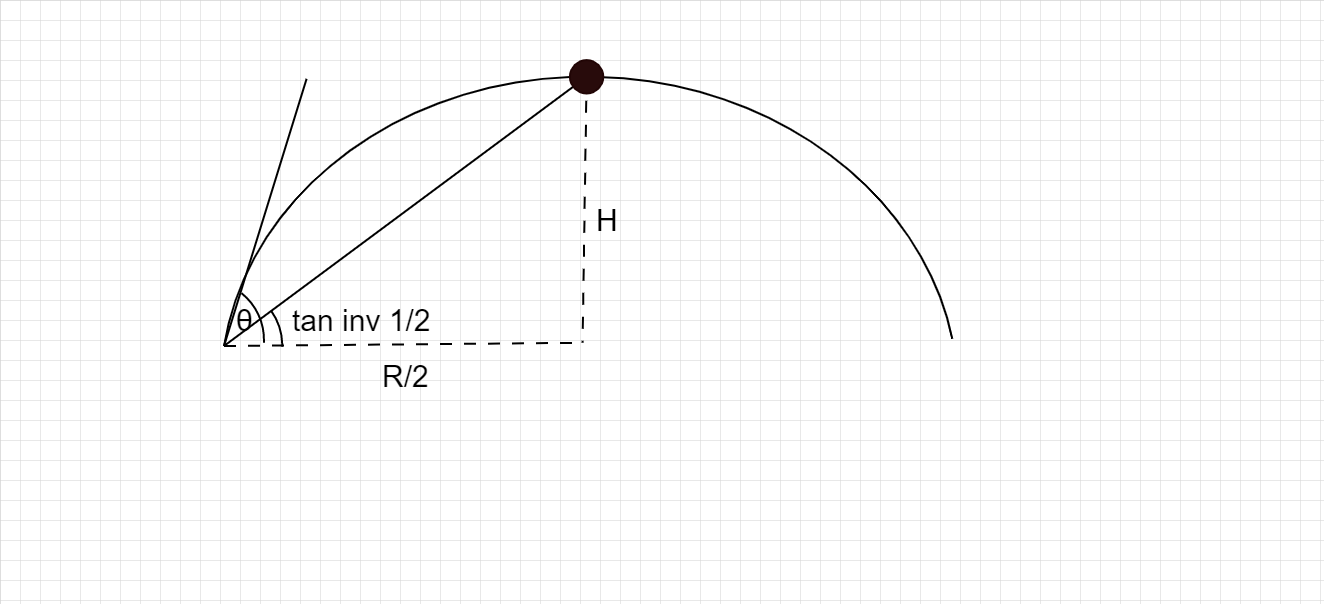
Thus, we can write-
$\Rightarrow \left( {\dfrac{1}{2}} \right) = \dfrac{H}{{R/2}} = \dfrac{{2H}}{R}$
As, \left\\{ {\tan \left( {{{\tan }^{ - 1}}\dfrac{1}{2}} \right) = \dfrac{1}{2}} \right\\}
Putting the values of H and R,
$\Rightarrow \left( \dfrac{1}{2} \right)=\dfrac{2\left( {}^{{{U}^{2}}{{\operatorname{Sin}}^{2}}\theta }/{}_{2g} \right)}{\left( {}^{2{{U}^{2}}\operatorname{Sin}\theta \cos \theta }/{}_{g} \right)}$
On canceling terms,
$\Rightarrow \left( {\dfrac{1}{2}} \right) = \dfrac{{\sin \theta }}{{2\cos \theta }}$
$\Rightarrow \dfrac{1}{2} \times 2 = \tan \theta$
$\Rightarrow \tan \theta = 1$
So, $\theta = 45^\circ$
Therefore, the correct answer is (B).

Additional Information
In projectile motion, the velocity has two components, horizontal and vertical. The vertical velocity is affected by the gravitational acceleration and thus increases and decreases over the course of the path and also makes the object to reverse its direction, resulting in a maximum height reached.
The horizontal component of velocity however is not affected by any acceleration (except drag force, which can be neglected in ideal cases). This is why the horizontal velocity remains constant throughout the flight, and suddenly becomes zero when the projectile path ends and the object hits the ground.

Note
The horizontal distance of the object from the point of projection should be taken half the value of range because this is the point where the object reaches the maximum height at that height. The equation of the path followed by a projectile is a parabola.