Question

An object is situated at $8\;cm$ from a convex lens of focal length $10\;cm$. Find the position and the nature of the image. Draw a ray diagram to illustrate the formation of the image-
(A) $- 40\;$
(B) $50\;$
(C) $60\;$
(D) $- 20\;$

Answer 1

The image formed by a convex lens can have different features, it can be enlarged or diminished, real or virtual, upright or inverted, the nature of the image formed depends on the position of the object relative to the lens.

Complete step by step solution:
It is given that,
The object is kept at a distance of $u = 8\;cm$ from the lens’ optical centre.
The focal length of the given lens is, $f = 10\;cm$
It is observed that the distance of the object is less than the focal length of the object.
For a convex lens, if the object is kept within the focal length of the lens, then the rays from the same point in the object (say, from the point$A$ ) diverge after the refraction from the lens. This creates a virtual image of the object and the image is situated behind the lens and is enlarged.
The ray diagram for the illustration of the formation of this image is drawn below-

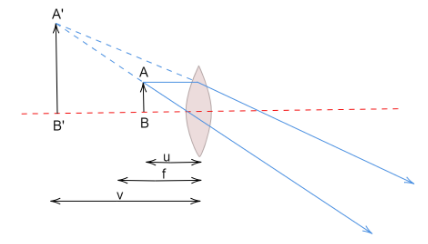
Let the distance of the image from the optical centre of the lens be $v$.
We can find the position of the image by using the lens formula-
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
We can rearrange this,
$\dfrac{1}{v} = \dfrac{1}{f} + \dfrac{1}{u}$
According to the sign convention, we have,
$u = - 8cm$
The focal length of a convex lens is taken as positive, therefore-
$f = 10cm$
Keeping these values in the lens formula-
$\dfrac{1}{v} = \dfrac{1}{{10}} + \left( { - \dfrac{1}{8}} \right)$
$\Rightarrow \dfrac{1}{v} = \dfrac{1}{{10}} - \left( {\dfrac{1}{8}} \right)$
Cross multiplying,
$\Rightarrow \dfrac{1}{v} = \dfrac{{8 - 10}}{{80}}$
$\Rightarrow \dfrac{1}{v} = \dfrac{{ - 2}}{{80}}$
Reciprocating,
$v = - 40$
The image is formed at a distance of $- 40cm$ from the optical centre of the lens. The negative sign signifies that the image is formed behind the lens.

Note:
The sign convention should be kept in mind while using the lens formula or the mirror formula in optics. For the position of an image, the sign tells whether the image is situated behind or above the lens. The terms behind or above are defined relative to the direction of travel of light.