Question

An object is put at a distance of $5cm$ from the first focus of a convex lens of focal length $10cm$ . If a real image is formed, its distance from the lens will be:
A.$15cm$
B.$20cm$
C.$25cm$
D.$30cm$

Answer 1

In case of real image formation the image is formed at the opposite side of the object, so we have to take the distance between object and lens negative because the object distance is calculated along the opposite direction of light.

Complete answer:
Let the distance between the object and the lens is $u$ and the distance between image and the lens is $v$ and the focal length of the convex lens is $f$ .
So for the formation of real image in convex lens the diagram will be

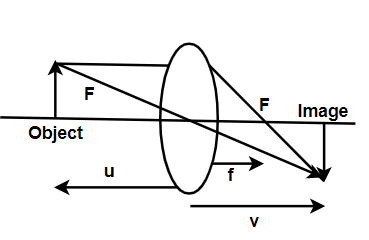
According to the question the object is placed at a distance of $5cm$ from first focus. And the distance of first focus from the lens is called the focal length. The focal length is $10cm$ .
So the object distance, $u = 5 + 10$ $cm$ $= 15cm$
Now the relation between $u,v$ and $f$ is
$\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$
Here $f = 10cm$ and for the real image $u = 15cm$ will be taken negative
Now putting the values in the above equation we get
$\dfrac{1}{v} - \dfrac{1}{{( - 15)}} = \dfrac{1}{{10}}$
$\Rightarrow \dfrac{1}{v} + \dfrac{1}{{15}} = \dfrac{1}{{10}}$
$\Rightarrow \dfrac{1}{v} = \dfrac{1}{{10}} - \dfrac{1}{{15}}$
$\Rightarrow \dfrac{1}{v} = \dfrac{1}{{30}}$
$\Rightarrow v = 30$
So the distance between the image and the lens is $30cm$ .

The correct answer is option D.

Note:
We can only get real images by concave mirrors and convex lenses if the object is placed further away from the mirror or lenses and the image is inverted. We have to take the distance always negative if it is in the opposite direction of light whether it is object distance or image distance or focal length.