Question

An object is put at a distance of 5 cm from the first focus of a convex lens of focal length 10 cm. If a real image is formed, its distance from the lens will be
(A) 15 cm
(B) 20 cm
(C) 25 cm
(D) 30 cm

Answer 1

Hint : We need to draw the image for the problem which will be helpful in the calculation. From the relationship between focal length, object distance and the image distance which is given as, $\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$ we can find the image distance by substituting the values.

Formula Used: In this solution we will be using the following formula,
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$ where $f$ is the focal length of the lens, $v$ is the image distance and $u$ is the object distance.

Complete step by step answer
A convex lens is one in which the rays of light that enter parallel to its principal axis converge at a single point on the opposite side. Real images are formed by the converging rays of light.
We need to be familiar with a few terms before we proceed. Lenses have two faces and allow light to pass through either face, no matter from which direction the light comes from. Focal point, F of the lens is a point at which parallel light rays incident on the lens converge. There are two focal points on either side of the lens. The distance from the centre of the lens (C) to the focal point (F) is the focal length(represented by $f$ ). Twice the focal length from the centre of curvature is the point, 2F. This is an imaginary point.

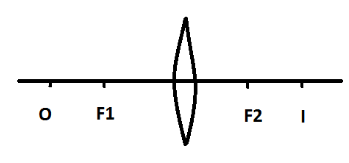
Let us consider the image given above. Let the focal length of the lens be $f$ . Let the object be represented by O and the image be represented by I.
It is given in the question that, $f = 10cm$
Let us assume that the distance of point O from F1 is ${x_1}$ and the distance of I from F2 is ${x_2}$ .
Let the distance of the object from the centre of the lens along the principal axis be $u$ and the distance of the image from the centre of the lens along the principal axis be $v$ .
$\therefore u = - \left( {f + {x_1}} \right)$
$\Rightarrow u = - 10 - 5 = - 15cm$
The value of $u$ is negative, since the object is on the left side of the lens.
$\therefore v = \left( {f + {x_2}} \right)$
The value of $v$ is positive, since the object is on the right side of the lens.
We know that,
$\Rightarrow \dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$ where $f$ is the focal length.
Substituting, the values of $v$ and $u$ ,
$\Rightarrow \dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u}$
$\Rightarrow \dfrac{1}{v} = \dfrac{{uf}}{{\left( {u + f} \right)}}$
Assigning the values of $u$ and $f$ we get,
$\Rightarrow \dfrac{1}{v} = \dfrac{{ - 15 \times 10}}{{\left( { - 15 + 10} \right)}}cm$
Thus, $v = 30cm$
$\therefore$ The correct answer is Option D.

Note
Converging lens magnifies images of the objects placed in front of them to produce erect, magnified images. Hence, these lenses are practically used as magnifying lenses in various places and also as eyeglasses to correct farsightedness.