Question

An object is placed in front of the plane mirror of length $L$ at a distance $d$ on its bisector line. An observer is at a perpendicular distance of $p$ from that mirror. If the observer is walking parallel to the mirror, up to what maximum possible distance he can observe the image of that object?
A. $L\left( {1 + \dfrac{d}{p}} \right)$
B. $L\left( {1 + \dfrac{p}{d}} \right)$
C. $p\left( {1 + \dfrac{L}{d}} \right)$
D. $p\left( {1 + \dfrac{d}{L}} \right)$

Answer 1

Draw a proper diagram to understand the question then we properties of the triangle to calculate the maximum distance travelled will be the distance bet two reflected rays.

Complete step by step answer: It is given in the question that the length of the plane mirror is L.
The object A is at a perpendicular distance P from the mirror.
Observe the diagram for reference.

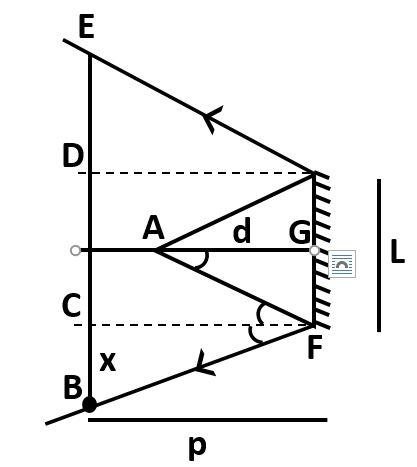
Let the maximum distance travelled by the observer be $y$.
Let C be the point in the straight line to the bottom of the plane mirror.
Let A be the point where the object is placed.
Let B be the extreme point where the observer can see the object in the mirror.
Now, the other extreme point from where the image can be seen be E.
Then from the diagram you can observe that the maximum distance the observer can cover such that he can see the object in the mirror will be BE.
Therefore, we can write.
Maximum distance $y = BC + CD + DE$
$= x + L + x$
$\Rightarrow y = L + 2x$ . . . . . . (1)
Now, Consider $\Delta AGF$and $\Delta FCB$
$\angle GAF = \angle AFC$ (Alternate interior angles)
since angle of incidence is equal to angle of reflection
$\angle AFC = \angle CFB$
$\therefore \angle GAF = \angle BFC$
$\angle AGF = \angle BCF = {90^0}$
Therefore, by AA criteria of similarity of triangle we get
$\Delta AGF \approx \Delta FCB$
Since the ratio of the corresponding sides of a triangle is equal. We can write
$\dfrac{{AG}}{{FC}} = \dfrac{{GF}}{{CB}}$
By substituting the values, we get
$\dfrac{d}{t} = \dfrac{{\dfrac{L}{2}}}{x}$
By cross multiplying we get
$x = \dfrac{{PL}}{{2d}}$
By substituting this values in equation (1) we get
$y = L + \dfrac{{PL}}{d}$
By taking common terms out , we get $y = L\left( {1 + \dfrac{P}{d}} \right)$
Therefore the maximum distance the observer can travel is $L\left( {1 + \dfrac{P}{d}} \right)$.

Note: For this question you had to understand that we can see any object when light falls on the objects and then falls in our eyes. So, the observer will not be able to see the object in the mirror once he crosses the point where the reflected ray is meeting the point B and Point E. Therefore, the maximum distance cannot be more than BE.