Question

An object is placed in front of a concave mirror of radius of curvature 15 cm, at a distance of 10cm. The position and nature of the image is formed
A. +30cm, virtual and erect
B. +30cm, real and inverted
C. -30cm, virtual and erect
D. -30cm, real and inverted

Answer 1

We use here mirror formula for a concave mirror. Concave mirror in which the inner depressed surface is reflecting and the outer surface is painted. It can produce both real and virtual images. The images can be enlarged, diminished, and the same size as the object.

Complete step by step answer:
Here the object is placed in the front of the concave mirror,
Radius of curvature (R) = -15cm
Object distance (u) = -10cm

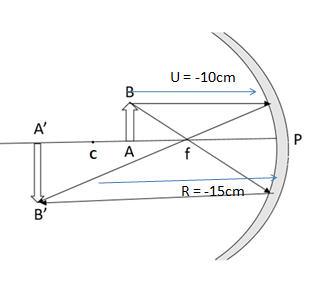
(Here we take negative signs by applying a new Cartesian sign convention.)
First we find the focal length of the concave mirror, ${\rm{f = }}\dfrac{{{\rm{ - R}}}}{2} = \dfrac{{ - 15}}{2}{\rm{cm}}$
Now by using mirror formula $\dfrac{1}{{\rm{u}}} + \dfrac{1}{{\rm{v}}} = \dfrac{1}{{\rm{f}}}$ we get,
$\dfrac{1}{{\rm{v}}} = \dfrac{1}{{\rm{f}}} - \dfrac{1}{{\rm{u}}}$
$\Rightarrow - \dfrac{2}{{15}} - \dfrac{1}{{({\rm{ - 10)}}}} = - \dfrac{2}{{15}} + \dfrac{1}{{10}} = - \dfrac{1}{{30}}$
$\dfrac{1}{{\rm{v}}} = - \dfrac{1}{{30}}$
$\Rightarrow {\rm{v = - 30cm}}$
Here $v$ is the image of an object and the image formed by the concave mirror is at 30cm in front of it.

Therefore the image is real and inverted. Thus correct option is (D).

Note:
A concave mirror is a converging mirror, which has a reflecting surface inwards. The concave mirror reflects light inward to one focal point. They are used to focus light—the concave mirror used as car headlights. The mirror formula is the same for a convex and concave mirror. Concave mirrors and plane mirrors are always used inside mirrors of automobiles. The image formed in the concave mirror is diminished, and it is typical to find precisely how far and closer away from the objects.