Question

An object is placed at a distance of $30\,cm$ in front of a convex mirror of focal length $15\,cm$ . Find the nature and the position of the image.

Answer 1

In this question, we will first calculate the image distance from the given object distance and focal length of the mirror using the mirror formula given as $\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$ where v is the image distance, u is the object distance and f is the focal length of the mirror.

Complete step by step answer:
Then, we shall calculate the magnification of the image formed and then from the sign of the image distance and the magnification, we will tell the nature and position of the image.
Complete step by step answer: The mirror formula is given by
$\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$ where v is the image distance, u is the object distance and f is the focal length of the mirror.
According to the question, we can say that,
$u = 30\,cm$ and $f = 15\,cm$
Substituting in the mirror formula we have,
$\dfrac{1}{v} + \dfrac{1}{{ - 30}} = \dfrac{1}{{15}}$
Rearranging the terms, we get,
$\dfrac{1}{v} = \dfrac{1}{{15}} + \dfrac{1}{{30}}$
Further solving the equation, we get,
$\dfrac{1}{v} = \dfrac{{30 + 15}}{{30 \times 15}}$
$\Rightarrow \dfrac{1}{v} = \dfrac{{45}}{{450}}$
$\Rightarrow \dfrac{1}{v} = \dfrac{1}{{10}}$
Taking reciprocal both sides, we get,
$v = 10\,cm$
Magnification is defined as the ratio of the image distance and the object distance. Mathematically it is expressed as $m = -\dfrac{v}{u}$ where m is the magnification, v is the image distance and u is the object distance.
In the given situation,
$u = -30\,cm$ and $v = 10\,cm$
Substituting the values we get,
$m = -\dfrac{{10}}{{-30}}$
$\Rightarrow m = \dfrac{1}{3}$
Magnification can also be defined as a ratio of the image size and the object size. This is expressed as
$m = \dfrac{h^{'}}{h}$ where $h^{'}$ is the image size and h is the object size.
In this situation we calculated the magnification to be one.
Substituting in the formula, we get,
$\dfrac{1}{3} = \dfrac{h^{'}}{h}$
$\Rightarrow h = 3h^{'}$

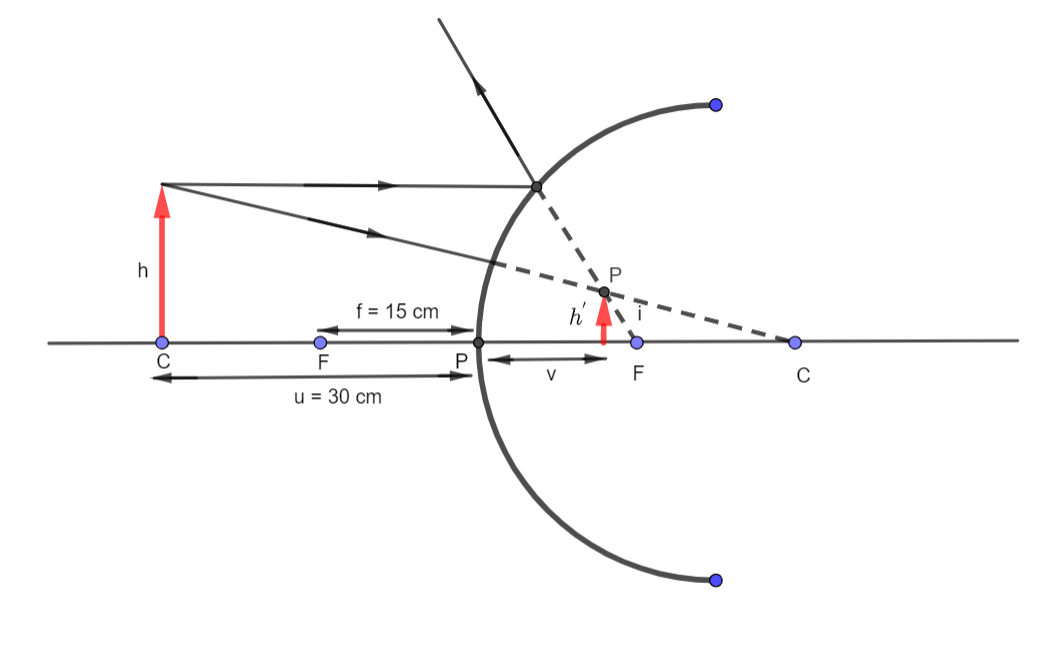
Hence, the characteristics of the image formed are:

1. Position: Since the focal length is $15\,cm$ and the image distance is $10\,cm$ , we can say that the image is formed between the pole and the focus of the mirror.
2. Nature: Since the sign of v came out to be positive, we can say that the image formed is virtual and erect.
3. Magnification: Since the magnification is less than one, we can say that the image is diminished.
   The image formation as depicted by a ray diagram in this case would be

Note:
We adopt a standard convention that the object is always kept at the left of the mirror and hence the light rays are incident on the left of the mirror. Here we took $u = - 30\,cm$ because the object is located at the left side of the mirror. The sign convention demands that the distances measured to the left of the pole of the mirror are to be taken negative. Following proper sign conventions would give the correct answer.