Question

An object is placed at a distance of 20 cm from a convex mirror or radius of curvature 40 cm. At what distance from the object should a plane mirror be placed so that the images due to mirror and plane mirror are in the same plane?
A) 15 cm
B) 30cm
C) 60cm
D) 40cm

Answer 1

In the plane mirror, the distance of the image from the plane mirror is equal to the distance of the object from the plane mirror. Convex mirror always forms a virtual, erect and diminished image. Therefore, the distance of the image is always less than the focal length and the image always lies between the pole and the focus of the convex mirror.

Formula used:
Focal length of the spherical mirror: $f = \dfrac{R}{2}$
Mirror Formula: $\dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u}$

Complete step by step solution:
The mirror is a highly polished surface from which the light is reflected. Spherical mirror is the part of the spherical surface polished either from the inner or outer side. Convex mirror is the spherical mirror polished from the outside. Light is incident on the bulged side of the mirror.
The radius of curvature and the object distance from the convex mirror are given as
R = 40cm
u = -20cm
Radius of curvature is the radius of the sphere whose mirror is the part.
The Focal length of the spherical mirror is given as:
$f = \dfrac{R}{2}$
Radius of curvature of the given convex lens is 40cm.
Therefore, $f = \dfrac{R}{2} = \dfrac{{40}}{2} = 20$cm
Using mirror formula to find the distance between image and pole of the convex mirror
$\dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u}$
where ‘v’ is the image distance from the pole.
Thus, $\dfrac{1}{{20}} = \dfrac{1}{v} + \dfrac{1}{{ - 20}}$
Substituting, $\dfrac{1}{v} = \dfrac{1}{{20}} + \dfrac{1}{{20}} = \dfrac{1}{{10}}$
Therefore v = 10cm
So, the distance between object and image is $u + v$ = 20+10 = 30cm

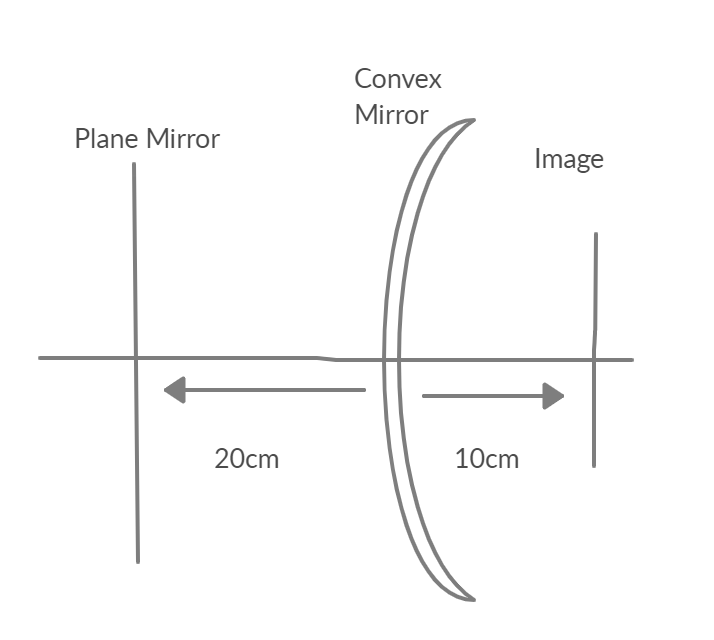
Thus, the distance from the object where a plane mirror must be placed so that the images due to mirror and plane mirror are in the same plane is $\dfrac{{30}}{2} = 15$cm.

So, the correct answer is “Option A”.

Note:
The center of curvature is not to be confused with the pole of the mirror. As spherical mirrors are formed by spherical surfaces, the center of curvature is the center of the sphere whose mirror is the part. And, the pole is the midpoint of the spherical mirror itself.
The image formed by a plane mirror is erect and virtual when the object is real and is inverted and real when the object is virtual.