Question

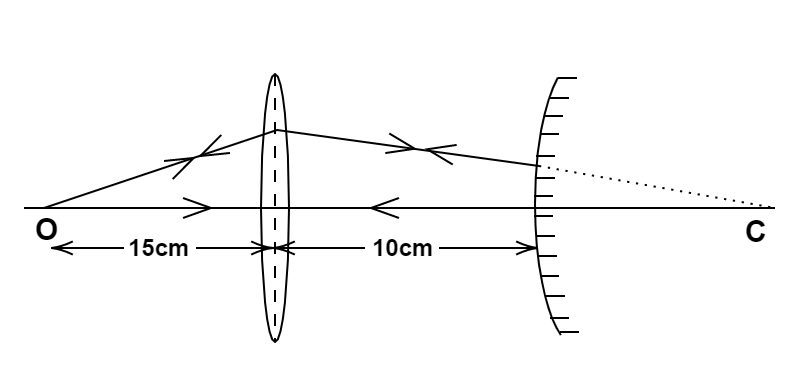
An object is placed at a distance of $15cm$ from a convex lens of focal length $10cm$ . On the other side of the lens, a convex mirror is placed at its focus such that the image formed by the combination coincides with the object itself. The focal length of the convex mirror is:
a. $20cm$
b. $10cm$
c. $15cm$
d. $30cm$

Answer 1

Use the lens formula to find image distance from object distance and focal length of the lens. After that subtract the distance of the convex lens from image distance. This will give a radius of curvature. Now, use the relation between the radius of curvature and focal length to get the focal length of the convex mirror.

Formula used:
$\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$ ........... $\left( 1 \right)$

Complete step by step answer:
Lens formula is given by,
$\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$
Where, $v$ : Image distance from the lens
$u$ : object distance from the lens
$f$ : Focal length of the lens
Given: $u = - 15cm$
$f = 10cm$

Distance between lens and mirror say $d = f = 10cm$
On substituting the given values in the equation $\left( 1 \right)$ we get,
$\dfrac{1}{v} + \dfrac{1}{{15}} = \dfrac{1}{{10}}$
$\Rightarrow \dfrac{1}{v} = \dfrac{1}{{10}} - \dfrac{1}{{15}}$
On solving the above equation for $v$ we get,
$\dfrac{1}{v} = \dfrac{5}{{150}} = \dfrac{1}{{30}}$
Taking the reciprocal on both sides,
$v = 30cm$
Thus the image will be formed $30cm$ to the right of the lens and it will be inverted.

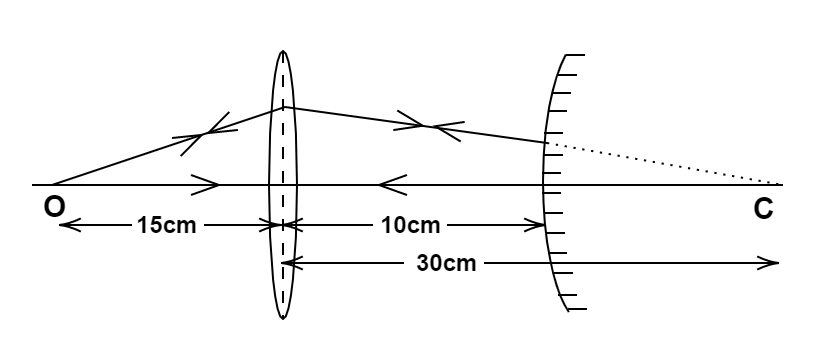
And so, the distance between the lens and mirror will be
$d$ = image distance-radius of curvature of the convex mirror
$d = v - R$
By substituting the values in the above equation we get,
$10 = 30 - R$
$\Rightarrow R = 20cm$

Let $f'$ be the focal length of the convex mirror
As we know, the radius of curvature $\left( R \right)$ is given by,
$R = 2f'$
On putting the value of $R$ we get,
$f' = \dfrac{{20}}{2}$
$\Rightarrow f' = 10cm$
As a result, the focal length of the convex mirror is $10cm$.

Hence, the correct answer is option (B).

Note: The sign conventions of the image, object, and focal length. In this problem, we take the object distance to be negative as the object is kept on the left side of the lens. If it was on the right side then the object distance would be positive. The image made due to the convex lens at the right side of the convex lens acts as a virtual image for the convex mirror.