Question

An object is placed at a distance of $12cm$ in front of a concave mirror. It forms a real image four times larger than the size of the object. Calculate the distance of the image of the object formed from the mirror.

Answer 1

In order to find the image distance of the object from the mirror, we will use the magnification concept. Magnification determines the relation between object size and image size and it can be written as $m = \dfrac{{image(size)}}{{object(size)}}$ . Which is the ratio of size of the image to the size of the object.

Complete step-by-step solution:
It’s given that the size of the image is four times larger than the object’s size. So we can write this as
Size of image $= 4$ (size of object).
In the case of mirrors we also have the general formula of magnification as $m = \dfrac{{ - v}}{u}$ where $v$ is the distance of image from mirror and $u$ is the distance of an object from mirror.
Given that, $u = - 12cm$
Let us draw the image formation, as light rays coming from object parallel to principal axes will reflected and pass through focus of concave mirror while rays falling on pole will reflected with same angle of incidence and point of intersection of these two rays is the point where image will be formed as shown in the diagram.

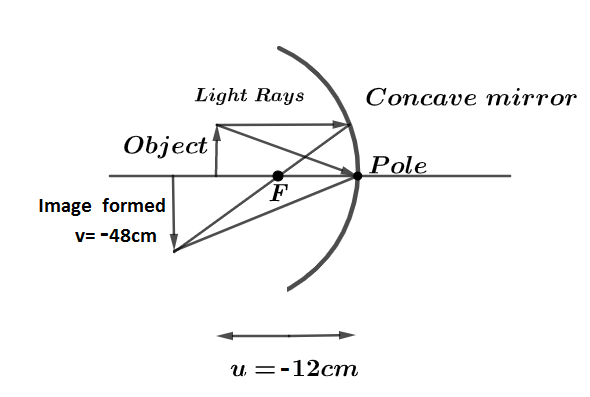
So using magnification formula we have:
$m = \dfrac{{image(size)}}{{object(size)}}$ $= \dfrac{{ - v}}{u}$
Or
$\dfrac{{ - v}}{u} = - 4$
$- v = - 4 \times ( - 12)$
$v = - 48cm$
Hence, the distance of image from the mirror is $48cm$ on the same side of the object.

Note: It should be noticed that, image is formed real and inverted hence magnification is negative and object lies left to the pole of mirror and image also lies at left of the pole and By new sign conventions any distance measured left to the pole of mirror is taken as negative while any distance measured to the right of pole is taken as positive.