Question

An object is observed from three points A, B and C in the same horizontal line passing through the base of the object. The angle of elevation at B is twice and at C thrice that of A. If AB = a, BC = b, then the height of the object is
a.$\dfrac{a}{2b}\sqrt{\left( a+b \right)\left( 3b-a \right)}$
b.$\dfrac{a}{2b}\sqrt{\left( a-b \right)\left( 3b-a \right)}$
c.$\dfrac{a}{2b}\sqrt{\left( a-b \right)\left( 3b+a \right)}$
d.$\dfrac{a}{2b}\sqrt{\left( a+b \right)\left( 3b+a \right)}$

Answer 1

Hint: Assume the angle of elevation at A be $\alpha$ . The angle of elevation at B and will be $2\alpha$ and $3\alpha$ respectively. Now, find $\angle PBA$ and $\angle PCA$ using a linear pair of angles. As we know that the sum of all angles of a triangle is $\pi$ , so using this find $\angle BPA$ and $\angle CPB$ . We will get BP=BA(sides opposite to equal angles are also equal). Now use the sine formula in the $\Delta PCB$ and get the value of $\sin \alpha$ . Using the identity, ${{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha =1$ , get the value of $\cos \alpha$ . We know that $\sin 2\alpha =2\sin \alpha \cos \alpha$ . In $\Delta PQB$ , apply $\sin 2\alpha$ . Then, put the value of $\sin \alpha$ , $\cos \alpha$ , and BP=a. Solve further and get the value of PQ.

Complete step-by-step answer:

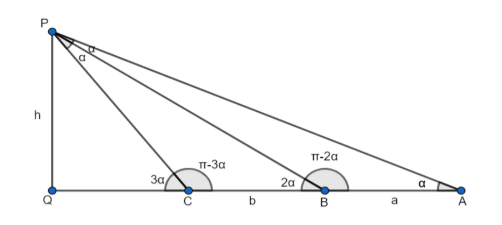
Let the angle of elevation at A be $\alpha$ .
$\angle PAQ=\alpha$ ……………………(1)
According to the question, it is given that the angle of elevation at B is twice and at C thrice that of A.
The angle of elevation at B that is $\angle PBQ$ = $2\alpha$ ………………….(2)
The angle of elevation at B that is $\angle PCQ$ = $3\alpha$ ………………………..(3)
$\angle PBQ+\angle PBA=\pi$ (linear pair)
From equation (2), we can write $\angle PBA=\pi -2\alpha$ ……………………………..(4)
Similarly, $\angle PCQ+\angle PCA=\pi$ (linear pair)
From equation (3), we can write $\angle PCA=\pi -3\alpha$ ……………………………..(5)
In $\Delta PBA$ , we have
$\angle BPA+\angle PAQ+\angle PBA=\pi \,(sum\text{ }of\text{ }all\text{ }angles\text{ }of\text{ }a\text{ }triangle\text{ }is\text{ }\pi )$ ………………………..(6)
Now, using equation (1) and equation (4), we can write equation (6) as,

& \angle BPA+\angle PAQ+\angle PBA=\pi \\\ & \Rightarrow \,\angle BPA+\alpha +\pi -2\alpha =\pi \\\ & \Rightarrow \angle BPA-\alpha =0 \\\ \end{aligned}$$ $$\Rightarrow \angle BPA=\alpha $$ ………………………….(7) In $$\Delta PCB$$ , we have $$\angle PCB+\angle CPB+\angle PBC=\pi \,(sum\text{ }of\text{ }all\text{ }angles\text{ }of\text{ }a\text{ }triangle\text{ }is\text{ }\pi )$$ ………………………..(8) Now, using equation (2) and equation (5), we can write equation (8) as, $$\begin{aligned} & \angle PCB+\angle CPB+\angle PBC=\pi \, \\\ & \Rightarrow \,\pi -3\alpha +\angle CPB+2\alpha =\pi \\\ & \Rightarrow \angle CPB-\alpha =0 \\\ \end{aligned}$$ $$\Rightarrow \angle CPB=\alpha $$ ………………………….(9) We know the sine formula of a triangle. We know the sine formula of a triangle, $$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}$$ . Now, applying sine formula in the $$\Delta PCB$$ , $$\dfrac{BC}{\sin \alpha }=\dfrac{PB}{\sin (\pi -3\alpha )}$$ We know the formula that, $$\sin 3\alpha =3\sin \alpha -4{{\sin }^{3}}\alpha $$ and $$\sin \left( \pi -\theta \right)=\sin \theta $$ . Using this formula, we get $$\Rightarrow \dfrac{b}{\sin \alpha }=\dfrac{PB}{\sin 3\alpha }$$ $$\begin{aligned} & \Rightarrow \dfrac{b}{\sin \alpha }=\dfrac{PB}{3\sin \alpha -4{{\sin }^{3}}\alpha } \\\ & \Rightarrow b(3-4si{{n}^{2}}\alpha )=PB \\\ \end{aligned}$$ We have, $$\angle BPA=\alpha $$ and $$\angle PAB=\alpha $$ . So, PB = BA = a (sides opposite to equal angles are equal). $$\begin{aligned} & \Rightarrow b(3-4si{{n}^{2}}\alpha )=a \\\ & \Rightarrow 3b-a=4b{{\sin }^{2}}\alpha \\\ \end{aligned}$$ $$\Rightarrow \dfrac{\left( 3b-a \right)}{4b}={{\sin }^{2}}\alpha $$ $$\Rightarrow \sqrt{\dfrac{\left( 3b-a \right)}{4b}}=\sin \alpha $$ ………………….(10) We know the identity, $${{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha =1$$ . Now putting the value of $$\sin \alpha $$ from equation (10) in the identity, we get $$\begin{aligned} & \Rightarrow \dfrac{\left( 3b-a \right)}{4b}+{{\cos }^{2}}\alpha =1 \\\ & \Rightarrow {{\cos }^{2}}\alpha =1-\dfrac{\left( 3b-a \right)}{4b} \\\ & \Rightarrow {{\cos }^{2}}\alpha =\dfrac{4b-3b+a}{4b} \\\ & \Rightarrow {{\cos }^{2}}\alpha =\dfrac{a+b}{4b} \\\ \end{aligned}$$ $$\Rightarrow \cos \alpha =\sqrt{\dfrac{a+b}{4b}}$$ ………………………(11) In $$\Delta PQB$$ , we have $$\dfrac{PQ}{BP}=\sin 2\alpha $$ $$\Rightarrow PQ=BP\sin 2\alpha $$ We have, $$\angle BPA=\alpha $$ and $$\angle PAB=\alpha $$ . So, PB = BA = a (sides opposite to equal angles are equal). $$\Rightarrow PQ=BA\sin 2\alpha $$ $$\Rightarrow PQ=a\sin 2\alpha $$ ……………………(12) We know the formula, $$\sin 2\alpha =2\sin \alpha \cos \alpha $$ . From equation (10), equation (11) and equation (12), we get $$\begin{aligned} & \Rightarrow PQ=a.2\sin \alpha \cos \alpha \\\ & \Rightarrow PQ=a.2\sqrt{\dfrac{\left( 3b-a \right)}{4b}}\sqrt{\dfrac{a+b}{4b}} \\\ & \Rightarrow PQ=2a\dfrac{\sqrt{\left( 3b-a \right)\left( a+b \right)}}{4b} \\\ & \Rightarrow PQ=\dfrac{a}{2b}\sqrt{\left( 3b-a \right)\left( a+b \right)} \\\ \end{aligned}$$ Hence, option (A) is the correct option. Note: To solve this question, one may think to apply tan formulas in the $$\Delta PQC$$ , $$\Delta PQB$$ , and $$\Delta PQA$$ . If we do so then we will get complex equations which will be difficult to solve. So, we don’t have to approach this question by applying a tan formula.