Question

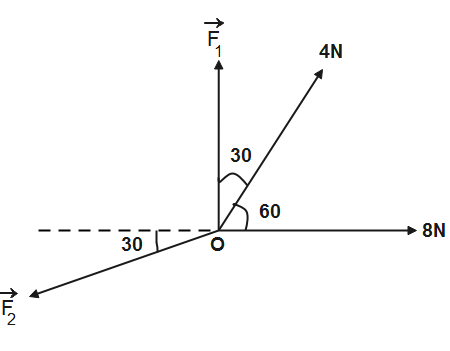
An object is in equilibrium under four concurrent forces in the directions shown in the figure. Find the magnitudes of $\overrightarrow{{{F}_{1}}}$ and $\overrightarrow{{{F}_{2}}}$.

Answer 1

Figure shows several forces acting on a particle. The sum of all forces is zero as the particle is in equilibrium. Resolving the forces into their perpendicular components and solving the equations, we can calculate the magnitude of both the unknown forces.

Complete answer:
When a body under the action of several forces is in equilibrium, it means that the sum of all the forces acting on it is zero. Force is a vector quantity, i.e. it has both magnitude as well as direction. Its SI unit is Newton (N).
It is given that the forces are concurrent therefore the line of action of all forces pass through the point O which is the position of the point.

Every vector is said to be made of two components which are perpendicular to each other and are such that the three vectors form the sides of a right angled triangle.
Resolving the given forces into its perpendicular components we get,

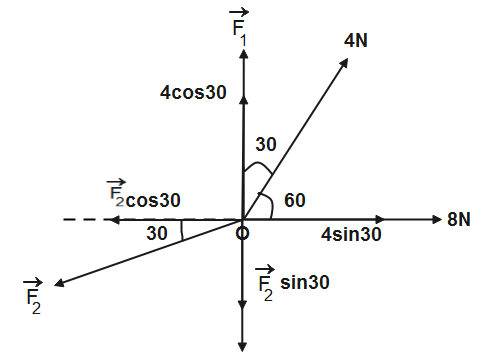
For the forces acting in along the y-axis-
$\begin{aligned} & \overrightarrow{{{F}_{1}}}+4\cos 30=\overrightarrow{{{F}_{2}}}\sin 30 \\\ & \Rightarrow \overrightarrow{{{F}_{1}}}+4\times \dfrac{\sqrt{3}}{2}=\dfrac{\overrightarrow{{{F}_{2}}}}{2} \\\ & \Rightarrow \overrightarrow{{{F}_{1}}}+2\sqrt{3}=\dfrac{\overrightarrow{{{F}_{2}}}}{2} \\\ \end{aligned}$
$\therefore \overrightarrow{{{F}_{2}}}-2\overrightarrow{{{F}_{1}}}=4\sqrt{3}$ - (1)
For all the forces acting along the x-axis-
$\begin{aligned} & \overrightarrow{{{F}_{2}}}\cos 30=4\times \sin 30+8 \\\ & \Rightarrow \overrightarrow{{{F}_{2}}}\times \dfrac{\sqrt{3}}{2}=4\times \dfrac{1}{2}+8 \\\ & \Rightarrow \overrightarrow{{{F}_{2}}}\times \dfrac{\sqrt{3}}{2}=10 \\\ \end{aligned}$
$\therefore \overrightarrow{{{F}_{2}}}=\dfrac{20}{\sqrt{3}}$ - (2)
Substituting eq (2) in eq (1), we get,
$\begin{aligned} & \dfrac{20}{\sqrt{3}}-2\overrightarrow{{{F}_{1}}}=4\sqrt{3} \\\ & \Rightarrow 20-2\sqrt{3}\overrightarrow{{{F}_{1}}}=12 \\\ & \therefore \overrightarrow{{{F}_{1}}}=\dfrac{4}{\sqrt{3}} \\\ \end{aligned}$
Therefore, the magnitude of $\overrightarrow{{{F}_{1}}}$ is $\dfrac{4}{\sqrt{3}}N$ and the magnitude of $\overrightarrow{{{F}_{2}}}$ is $\dfrac{20}{\sqrt{3}}N$.

Note:
Since the net force on the particle is zero, the particle has no acceleration this means that it is either at rest or moves in uniform motion. According to Newton’s second law of motion, the magnitude of force is determined by mass and acceleration. Concurrent forces means they pass through the same point.