Question
Question: An object consists of a uniform ring of radius R and a uniform chord AB (not necessarily made of the...
An object consists of a uniform ring of radius R and a uniform chord AB (not necessarily made of the same material) as shown. Which of the following cannot be the centre of mass of the object?
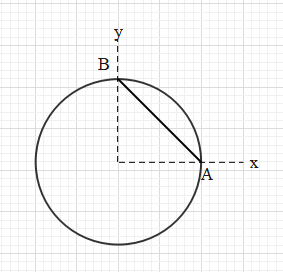
A. (R/3,R/3)
B. (R/2,R/2)
A. (R/4,R/4)
D. None of the above.
Solution
First find the centre of masses of the ring and the chord by using the fact that for a body with a uniform mass distribution, the centre of mass is located at the geometric centre of the body. Then find the centre of mass of the system by using the formulas for the x and y coordinates of the centre of mass of a system of two bodies. i.e.
xcom=M+M′Mx1+M′x2 and ycom=M+M′My1+M′y2.
Formula used:
Midpoint formula :- x=2x1+x2 and y=2y1+y2
xcom=M+M′Mx1+M′x2 and ycom=M+M′My1+M′y2
Complete answer:
Centre of mass of a body or a system is the point where all the mass of the body appears to be concentrated.
For a body with a uniform mass distribution, the centre of mass is located at the geometric centre of the body.
In the question, it is given that the object consists of a uniform ring and a uniform chord AB. Let us treat these two as different objects.
Let us find the centre of masses of the ring and the chord AB. It is given that the both objects have uniform mass distribution. Hence, the centre masses of both the objects will lie at the geometric centres of the two respectively.
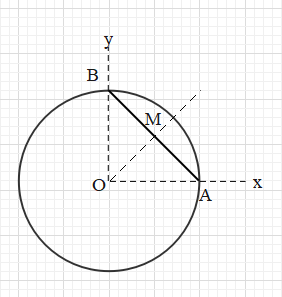
Therefore, the centre of mass of the circular ring is situated at its centre, i.e. at point O.
The centre of the rod is the midpoint of chord AB. Therefore, the centre of mass of the rod is situated at the midpoint of chord AB.
Suppose the radius of the ring is R. Therefore, the coordinates of the points A and B are (0,R) and (a,R) respectively.
The coordinates (x,y) of a midpoint of a line segment with endpoints as (x1,y1) and (x2,y2) are given as and y=2y1+y2.
In this case, x=20+R=2R and y=2R+0=2R.
Therefore, the coordinates of the midpoint of AB are (2R,2R).
Hence, the centre of mass of the ring is at O (0,0) and the centre of mass of the chord is at (2R,2R).
Let the mass of the ring be M and mass of the chord bM’.
Now, we can consider that there are two point sized bodies of mass M at (0,0) and mass M’ at (2R,2R).
The coordinates of the centre of mass of a system of two particle is given as
xcom=M+M′Mx1+M′x2 and ycom=M+M′My1+M′y2.
Here, (x1,y1) are the coordinates of M and (x2,y2) are the coordinates of M’.
Therefore, the x and y coordinates of the centre of mass the given system are:
xcom=M+M′M(0)+M′(2R)=M+M′M′(2R) and ycom=M+M′M(0)+M′(2R)=M+M′M′(2R)
As you can see that the x and y coordinates of the centre of mass can be any real value depending on the masses of the ring and the chord. However, the x and y coordinates will always be the same.
If we check the given options, in each of the first three options the coordinates are the same. Therefore, all the three options can be the centre of mass of the system.
So, the correct answer is “Option D”.
Note:
We found that the centre of masses of the ring and the chord are located at O (0,0) and at M (2R,2R).
Note that the centre of mass of these two bodies will lie on the line joining the points O and M. Depending on the masses of the ring and the chord the position of the centre of mass will change but it will always lie on this line.
The slope of this line is 1. Therefore, we can comment that the coordinates of each point lying on this are equal.
