Question
Question: An object consists of a uniform ring of radius R and its uniform chord AB (not necessarily made of t...
An object consists of a uniform ring of radius R and its uniform chord AB (not necessarily made of the same material) as shown. Which of the following cannot be the center of mass of the object?
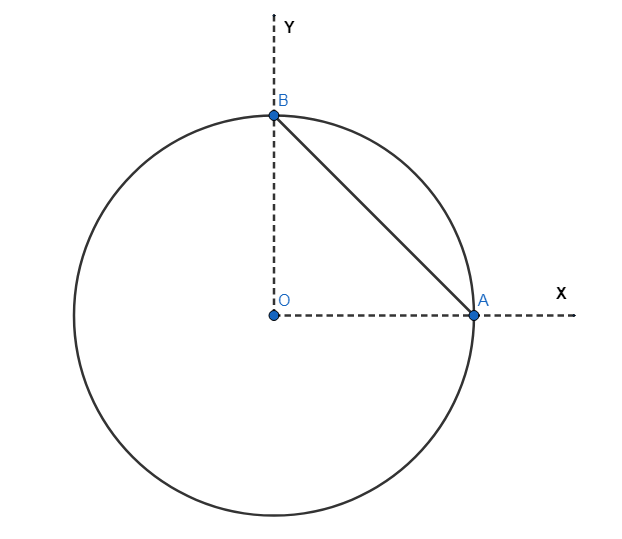
A. (3R,3R)B. (3R,2R)C. (4R,4R)D. (2R,2R)
Solution
Hint: The center of mass of a uniform object always lies at its center or centroid. For a uniform ring, it is at the center, and for a uniform rod, it is at the center of the rod.
Complete step by step answer:
We have a uniform ring of radius R and a uniform chord AB not made of the same material as the ring. So as we all know for a uniform body with uniform mass distribution, the center of mass of the body will lie at the centre of the body.
So if we consider only the ring of radius R and centered at the origin O, then the center of mass of the ring will lie at the center O which is also the origin.
If we are considering a uniform chord of length L, then the center of mass will lie on the midpoint of the rod.
So coming to our question, we have a uniform ring and a uniform chord of a different material than the ring. So the center of mass of the ring will lie at the center O of the ring. The chord AB can be taken as a uniform rod whose endpoints are given by the coordinates (0, R) and (R, 0). So the center of mass will lie at the center of a chord whose coordinates are given by (2R,2R).
So the masses said to be concentrated at the origin (0,0) and at the midpoint of the chord AB at (2R,2R). So the center of mass of both the ring and the chord will lie on a line that connects the center O and the midpoint of the chord AB. So the line that connects these two points is the line given by the equation y=x, which means that the x coordinate and the y coordinate will be the same. Refer to the figure given below for a clear idea.
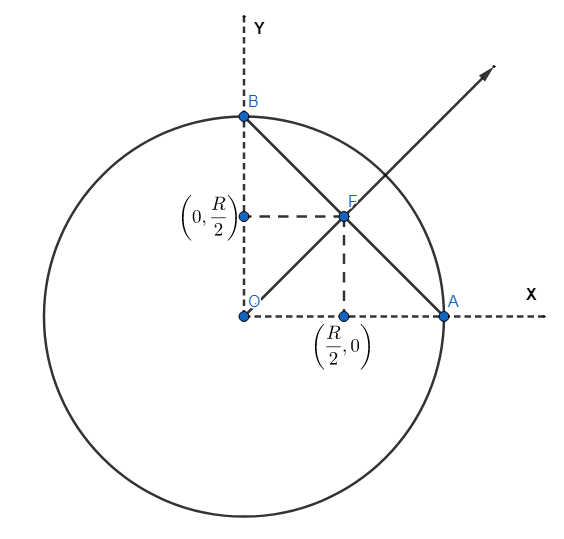
So the center of mass can lie on the line y=x. It can lie at any point on the line depending on the material used to make the ring and the chord.
Let us look at the other options to understand what that means, in option (A) (3R,3R), both the x-coordinate and y-coordinate are same. So, it satisfies the equation of the line; therefore, it is a possible coordinate where the center of mass can lie. In option (C) (4R,4R), the coordinate satisfies the condition of the straight line on which the center of mass can lie, so it can be a possible coordinate where the center of mass is located. Coming to option (D) (2R,2R), the coordinates satisfy the condition of the line and are a possible coordinate for the center of mass to be located.
Our question was to find out the coordinates from the options which do not satisfy the coordinate for the center of mass. So, in the options, the only option which violates this condition is option (B).
So the answer to our question is option (B)- (3R,2R).
Note: All the other options have the same x and y coordinate, so it satisfies the y=x condition.
For simple rigid objects, the center of mass will be situated at the centroid.
A center of mass of a body can be considered as a point in the body to which a force can be applied such that it will result in the production of a linear acceleration without an angular acceleration in the body.
