Question

An object and a screen are mounted on an optical bench and a converging lens is placed between them so that a sharp image is received on the screen. The linear magnification of the image is$\;2.5$. The lens is now moved $30\;cm$ nearer the screen and a sharp image is again formed on the screen. The focal length of the lens is:
A. $14.0\;cm$
B. $14.3\;cm$
C. $14.6\;cm$
D. $14.9\;cm$

Answer 1

Use the given linear magnification to arrive at the image distance in terms of the object distance. Then use the lens formula to arrive at an expression for the focal length of the lens, which you can plug into the expression arising from applying the lens formula to the case when the lens is moved towards the screen and consequently obtain the object distance. Plug this back into the focal length expression to arrive at an appropriate value for the same.

Formula used:
Magnification of a converging lens $m = \dfrac{v}{u}$
Lens formula for converging lens: $\dfrac{1}{f} = \dfrac{1}{v} +\dfrac{1}{u}$

Complete step-by-step answer:
We know that a converging lens is nothing but a convex lens that is placed between the object and the screen upon which the image is formed.
Let the focal length of the converging lens be$\;f$. Let the distance of the object from the lens be$\;u$ and the distance of the image from the lens be$\;v$.

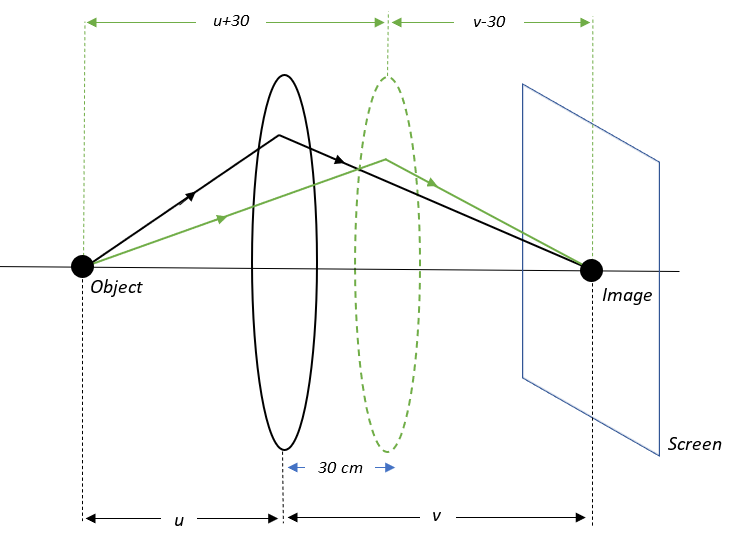
We are given that the linear magnification of the image is$\;2.5$, i.e.,
$m = \dfrac{v}{u} = 2.5 \Rightarrow v = 2.5u$
We can now obtain an expression for the focal length of the lens using the converging lens formula:
$\dfrac{1}{f} = \dfrac{1}{v}+\dfrac{1}{u} = \dfrac{1}{2.5u}+\dfrac{1}{u} = \dfrac{u+2.5u}{2.5u^2}$ $\Rightarrow \dfrac{1}{f} = \dfrac{3.5}{2.5u}$
Now, we are given that the lens is moved $30\;cm$ towards the screen and the image is still formed on the screen.
This means that the distance of the object from the lens will now be $u^{\prime} = u+30$ and the distance of the image from the lens becomes $v^{\prime} = v-30 = 2.5u-30$.
The converging lens formula thus becomes:
$\dfrac{1}{f} = \dfrac{1}{v^{\prime}} + \dfrac{1}{u^{\prime}} = \dfrac{1}{2.5u-30}+\dfrac{1}{u+30}$
Since the focal length of the lens remains unchanged, we can plug in the expression for $\dfrac{1}{f}$ we got from the initial case to get:
$\dfrac{3.5}{2.5u} = \dfrac{1}{2.5u-30} + \dfrac{1}{u+30} = \dfrac{(u+30)+(2.5u-30)}{(2.5u-30)(u+30)}$
$\Rightarrow \dfrac{3.5}{2.5u}= \dfrac{3.5u}{(2.5u-30)(u+30)}$
$\Rightarrow 3.5 \times (2.5u-30)(u+30) = 3.5u \times 2.5u$
$\Rightarrow (2.5u^2 + 75u – 30u - 900) = 2.5u^2$
$\Rightarrow 45u = 900 \Rightarrow u = 20\;cm$
Plugging this value of object distance into the focal length expression we get:
$\dfrac{1}{f} = \dfrac{3.5}{2.5u}$
$\Rightarrow f = \dfrac{2.5u}{3.5} = \dfrac{2.5 \times 20}{3.5} = 14.29\;cm \approx 14.3\;cm$

So, the correct answer is “Option B”.

Note: It is a common mistake to interchangeably use the terms enlarged and magnified. Note that enlarged means that the image is bigger relative to the object, whereas magnified can imply either an enlarged image or a diminished image. This is usually defined as magnification and is quantitatively expressed as:
$Magnification\; M = \dfrac{Image\;height}{Object\;height}$ or $M = \dfrac{v}{u}$
If $M <1$ then the image is diminished, and if $M>1$ then the image is enlarged. If $M=1$ it means there is no magnification and the image is the same size as that of the object.