Question

An object and a screen are mounted on an optical bench and a converging lens is placed between them so that a sharp image is received on the screen. The linear magnification of the image is 2.5. The lens is now moved 30 cm nearer to the screen and a sharp image is again formed on the screen. Find the focal length of the lens.
A) 14.0 cm
B) 14.3 cm
C) 14.6 cm
D) 14.9 cm

Answer 1

The lens used is a converging lens i.e., a convex lens. The focal length of the lens does not change as the lens is brought closer to the screen. The linear magnification refers to the ratio of the image distance to the object distance. The thin lens formula can be utilised to find the focal length of the lens.

Formulas used:
-The magnification of a lens is given by, $m = \dfrac{v}{u}$ where $v$ is the distance of the image from the lens and $u$ is the distance of the object from the lens.
-The thin lens formula is given by, $\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$ where $f$ is the focal length of the lens, $v$ is the image distance and $u$ is the object distance.

Complete step by step answer.
Step 1: Sketch a ray diagram representing the two cases.

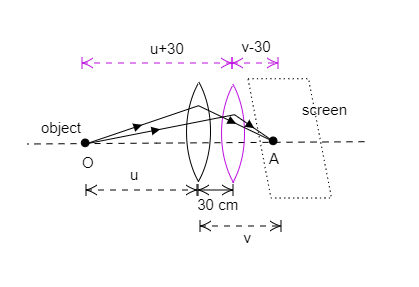
In the above diagram, the object is placed at O at a distance $u$ from the lens and the image is formed at point A on the screen, at a distance $v$ from the lens. But when the lens is placed closer to the screen, the image distance and object distance will be from the new position of the lens and hence will be different.
Let $f$ be the focal length of the lens which is to be determined.
The linear magnification is given to be 2.5.
Since the magnification of a lens is given by, $m = \dfrac{v}{u} = 2.5$, we can obtain a relation,
$v = 2.5u$ ---------(1).
Step 2: Express the thin lens formula for the initial position of the converging lens to obtain a relation for its focal length.
The thin lens formula is given by, $\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
where $f$ is the focal length of the lens, $v$ is the image distance and $u$ is the object distance.
For the converging lens, the thin lens formula will be $\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{{ - u}}$ or $\dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u}$ -------- (2)
Substituting equation (1) in equation (2) we get, $\dfrac{1}{f} = \dfrac{1}{{2.5u}} + \dfrac{1}{u}$
Simplifying we obtain, $\dfrac{1}{f} = \dfrac{{1 + 2.5}}{{2.5u}} = \dfrac{{3.5}}{{2.5u}}$
Therefore the focal length of the lens is given by, $\dfrac{1}{f} = \dfrac{{3.5}}{{2.5u}}$ --------- (3).
Step 3: Express the thin lens formula when the lens is moved closer to the screen.
When the lens is moved 30 cm nearer to the screen, the object distance becomes $u + 30$ while, image distance becomes $v - 30$ .
Then the thin lens formula for the new position of the lens will be $\dfrac{1}{f} = \dfrac{1}{{v - 30}} + \dfrac{1}{{u + 30}}$ -------(4)
Substituting equation (1) in equation (4) we get, $\dfrac{1}{f} = \dfrac{1}{{\left( {2.5u - 30} \right)}} + \dfrac{1}{{\left( {u + 30} \right)}}$
Simplifying we get, $\dfrac{1}{f} = \dfrac{{\left( {u + 30} \right) + \left( {2.5u - 30} \right)}}{{\left( {2.5u - 30} \right)\left( {u + 30} \right)}}$ or $\dfrac{1}{f} = \dfrac{{3.5u}}{{\left( {2.5u - 30} \right)\left( {u + 30} \right)}}$ --------- (5)
Substituting for equation (3) in equation (5) we get, $\dfrac{{3.5}}{{2.5u}} = \dfrac{{3.5u}}{{\left( {2.5u - 30} \right)\left( {u + 30} \right)}}$
On cancelling out the similar terms and on cross multiplying the equation becomes, $2.5{u^2} + 75u - 30u - 900 = 2.5{u^2}$
The above equation then reduces to give $45u = 900$ or $u = \dfrac{{900}}{{45}} = 20{\text{cm}}$
Thus the object distance is $u = 20{\text{cm}}$ .
Now substituting the value for $u = 20{\text{cm}}$ in equation (3) we get, $\dfrac{1}{f} = \dfrac{{3.5}}{{2.5 \times 20}} = 0.07{\text{c}}{{\text{m}}^{ - 1}}$ and on taking the reciprocal we get, $f = \dfrac{1}{{0.07}} = 14.3{\text{cm}}$
So, the focal length of the converging lens is $f = 14.3{\text{cm}}$ .

Hence the correct option is B.

Note: By sign convention, for a converging lens, the object distance $u$ is negative as the object is placed to the left of the lens and image distance $v$ is positive as the image is formed on the screen placed to the right of the converging lens. The focal length is positive for the converging lens.