Question

An object and a convex lens are approaching each other with speeds $3cm{s^{ - 1}}$ and $1cm{s^{ - 1}}$ on the principal axis as shown. Focal length of lens is $10cm$ . The speed of image relative to ground frame of reference is

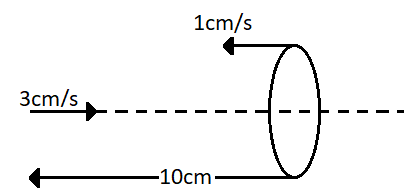
(A) $2cm{s^{ - 1}}$
(B) $3cm{s^{ - 1}}$
(C) $1cm{s^{ - 1}}$
(D) $15cm{s^{ - 1}}$

Answer 1

Hint : To solve this question, we need to use the lens equation. We have to differentiate the equation with respect to time to get a relation between the speeds of the object and image, relative to the lens.

Formula used: The formula used to solve this question is given by
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$ , here $f$ is the focal length of a lens, $v$ is the image distance, and $u$ is the object distance.

Complete step by step answer
In the given question, we have been given a convex lens of focal length $10cm$ , to which an object is approaching. So the image distance and the object distance are related by the lens formula which is given as
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$ …………...(1)
Since the focal length of a convex lens is taken as positive, so we substitute $f = + 10cm$ in the above formula to get
$\dfrac{1}{{10}} = \dfrac{1}{v} - \dfrac{1}{u}$
In the figure given in the question, the object is situated at a distance of $15cm$ from the lens. According to the sign convention, the object distance from the lens becomes $u = - 15cm$ . Substituting this above we get
$\dfrac{1}{{10}} = \dfrac{1}{v} + \dfrac{1}{{15}}$
$\Rightarrow \dfrac{1}{v} = \dfrac{1}{{10}} - \dfrac{1}{{15}}$
Taking LCM
$\dfrac{1}{v} = \dfrac{{3 - 2}}{{30}}$
$\Rightarrow \dfrac{1}{v} = \dfrac{1}{{30}}$
Taking the reciprocal we get
$v = 30cm$ …………...(2)
Now, we differentiate (1) with respect to the time $t$ to get
$\dfrac{{d\left( {1/f} \right)}}{{dt}} = \dfrac{{d\left( {1/v} \right)}}{{dt}} - \dfrac{{d\left( {1/u} \right)}}{{dt}}$
$\Rightarrow - \dfrac{1}{{{f^2}}}\dfrac{{df}}{{dt}} = - \dfrac{1}{{{v^2}}}\dfrac{{dv}}{{dt}} - \left( { - \dfrac{1}{{{u^2}}}\dfrac{{du}}{{dt}}} \right)$
We know that the focal length of a lens is constant, so we have $\dfrac{{df}}{{dt}} = 0$ . Substituting this above, we get
$0 = - \dfrac{1}{{{v^2}}}\dfrac{{dv}}{{dt}} + \dfrac{1}{{{u^2}}}\dfrac{{du}}{{dt}}$
$\Rightarrow \dfrac{1}{{{u^2}}}\dfrac{{du}}{{dt}} = \dfrac{1}{{{v^2}}}\dfrac{{dv}}{{dt}}$ …………...(3)
According to the question, the object and the lens are approaching each other with the speeds of $3cm{s^{ - 1}}$ and $1cm{s^{ - 1}}$ respectively. So the speed of the object with respect to the lens becomes
${v_{OL}} = \left( {3 + 1} \right)cm{s^{ - 1}} = 4cm{s^{ - 1}}$
Now, as the distance between the object and the lens is getting decreased, so we have
$\dfrac{{du}}{{dt}} = - {v_{OL}}$
$\Rightarrow \dfrac{{du}}{{dt}} = - 4cm{s^{ - 1}}$ ………….(4)
Substituting (4) in (3) we get
$- \dfrac{4}{{{u^2}}} = \dfrac{1}{{{v^2}}}\dfrac{{dv}}{{dt}}$
As $u = - 15cm$ , and from (2) $v = 30cm$ , so we have
$- \dfrac{4}{{{{\left( { - 15} \right)}^2}}} = \dfrac{1}{{{{30}^2}}}\dfrac{{dv}}{{dt}}$
$\dfrac{{dv}}{{dt}} = - 4 \times \dfrac{{{{30}^2}}}{{{{15}^2}}}$
On solving we finally get
$\dfrac{{dv}}{{dt}} = - 16cm{s^{ - 1}}$
So the speed of the image with respect to the lens is
${v_{IL}} = 16cm{s^{ - 1}}$ ……………..(5)
Let the speed of the image and that of the lens with respect to the ground be $v$ and ${v_L}$ respectively. We know when the object moves towards the lens, the image moves away from the lens. The image will be formed at the right of the lens, so for getting separated from the lens, the image must be moving towards the right. But the lens is moving towards the left, according to the question. So we have
${v_{IL}} = v + {v_L}$
The speed of the lens is given to be ${v_L} = 1cm{s^{ - 1}}$ . Also from (5) we have ${v_{IL}} = 16cm{s^{ - 1}}$ . Substituting these above we get
$16 = v + 1$
$\Rightarrow v = 15cm{s^{ - 1}}$
Thus, the speed of image relative to the ground is equal to $15cm{s^{ - 1}}$ .
Hence, the correct answer is option D.

Note
We should take care about the proper signs of the focal length, the image and the object distances according to the Cartesian sign convention. Also, take proper care while deciding the direction of the velocities of the image and the object.