Question

An object A of mass $m$ with initial velocity $u$ collides with a stationary object B. After elastic collision, A moves with $\dfrac{u}{4}$ . Calculate the mass of B.
(A) $\dfrac{{7m}}{5}$
(B) $\dfrac{{3m}}{5}$
(C) $\dfrac{{9m}}{5}$
(D) $\dfrac{{4m}}{5}$

Answer 1

Hint : It is known that for an elastic collision total energy and momentum due to collision is always conserved. Use conservation of momentum to find the mass of B. The conservation of momentum states that the momentum of a system in collision is always a constant of motion.

Complete Step By Step Answer:
We have given here that, the object A of mass $m$ with initial velocity $u$ collides with a stationary object B. Hence, initial velocity of B is zero. Now, after collision the velocity of the object A becomes, $\dfrac{u}{4}$ .Since, the collision was an elastic collision hence, the velocity of the objects will be conserved also. Let's say, the velocity of the object B of mass $M$ is $v$ .

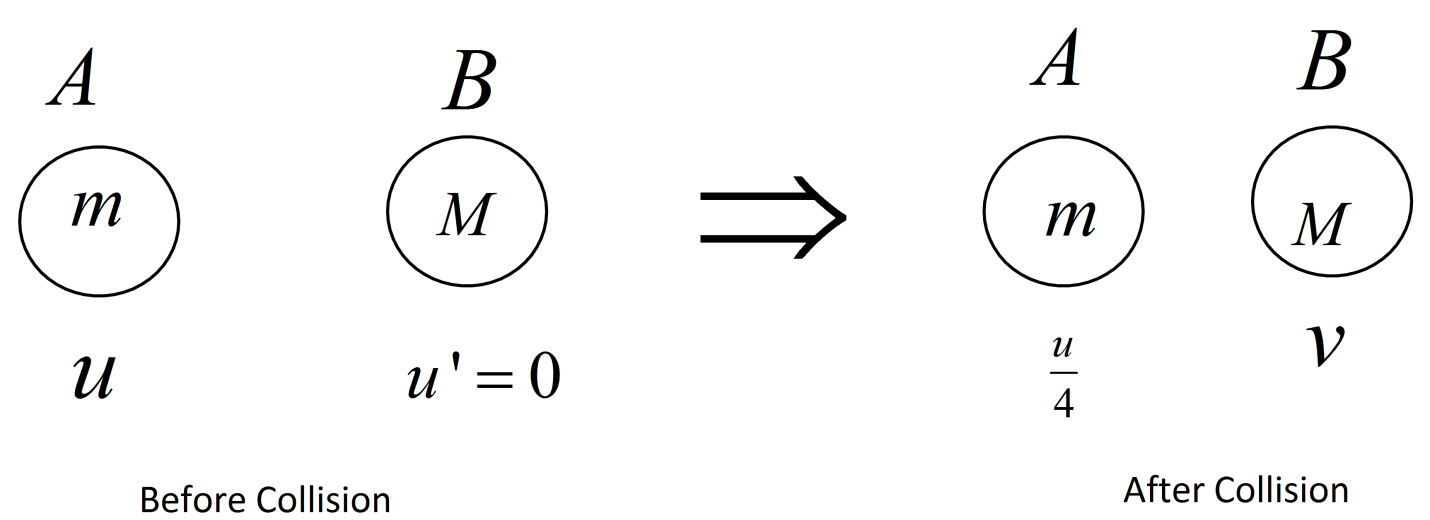
Hence, we can write,
$u - 0 = v - \dfrac{u}{4}$
Or, $v = u + \dfrac{u}{4}$
So, we get, $v = \dfrac{{5u}}{4}$
Now, from conservation of momentum we know that momentum of the collision is conserved. Hence, momentum after collision is equal to the momentum before collision
So, we can write, $mu + 0 = Mv + m\dfrac{u}{4}$
So, putting the value of the final velocity of the object B, $v = \dfrac{{5u}}{4}$ we get,
$mu + 0 = M\dfrac{{5u}}{4} + m\dfrac{u}{4}$
Simplifying further we get,
$M\dfrac{{5u}}{4} = \dfrac{{3mu}}{4}$
Hence, $M = \dfrac{{3m}}{5}$
Hence, the mass of the object B will be, $\dfrac{{3m}}{5}$ .
Hence, option (B ) is correct.

Note :
Conservation of mechanical energy states that the total mechanical energy of a system due to an elastic collision is always constant. If the potential energy of the system is taken to be constant then we can write, ${(KE)_{1i}} + {(KE)_{2i}} = {(KE)_{1f}} + {(KE)_{2f}}$ . Where, ${(KE)_{1i}}$ is the initial kinetic energy of first particle, ${(KE)_{2i}}$ is the initial kinetic energy of second particle, ${(KE)_{1f}}$ is the final kinetic energy of first particle and ${(KE)_{2f}}$ is the kinetic energy of second particle.