Solveeit Logo
Login

Question

Question: An object \(50\,cm\) tall is placed on the principal axis of a convex lens, its \(20\,cm\) tall imag...

An object 50 cm50\,cm tall is placed on the principal axis of a convex lens, its 20 cm20\,cm tall image is formed on the screen placed at a distance of 10 cm10\,cm from the lens. Calculate the focal length of the lens.

Explanation

Solution

In the question, we have given the value of the distance of the image from the lens, the height of the object, and its image. We are required to find the focal length of the lens and to find that we will use the formula of magnification and lens.

Complete answer:
Given:
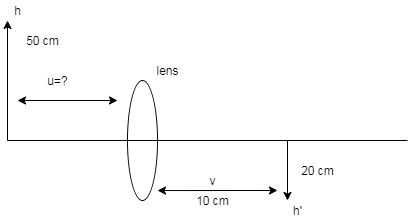
Height of object (h) = 50 cm=\,50\,cm
Height of image (h’) = −20 cm=\,-20\,cm(real and inverted as shown in the diagram below)
Distance of image from the lens (v) =10 cm=10\,cm
Distance of object from the lens (u) =?=?
Focal length of the lens (f) =?=?
Diagram:

We know that magnification (m) of the lens is given by:
m=vu=h′h    .....(1)m=\dfrac{v}{u}=\dfrac{h'}{h}\,\,\,\,.....(1)
Where, magnification (m) is the process of enlarging the apparent size, not physical size, of something. This enlargement is quantified by a calculated number also called "magnification". When this number is less than one, it refers to a reduction in size, sometimes called de-magnification.
Thus, substituting the values of h, h’ and v in equation (1), we get:
10u=−2050\dfrac{10}{u}=\dfrac{-20}{50}
u=−5020×10u=\dfrac{-50}{20}\times 10
Therefore,
u=−25 cmu=-25\,cm
Now, using the lens formula:
1v−1u=1f    .....(2)\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}\,\,\,\,.....(2)
Thus, substituting the values of v and in equation (2), we get:
⇒\Rightarrow 110−1−25=1f\dfrac{1}{10}-\dfrac{1}{-25}=\dfrac{1}{f}
⇒\Rightarrow 110+125=1f\dfrac{1}{10}+\dfrac{1}{25}=\dfrac{1}{f}
⇒\Rightarrow 5+25=1f\dfrac{5+2}{5}=\dfrac{1}{f}
Therefore,
f=507f=\dfrac{50}{7}
Or
f=7.14 cmf=7.14\,cm
Hence the focal length of the lens = 7.14 cm.=\,7.14\,cm.

Note:
To solve this kind of question we should have knowledge about ray optics. The focal length of an optical system is a measure of how strongly the system converges or diverges light; it is the inverse of the system's optical power. A positive focal length indicates that a system converges light, while a negative focal length indicates that the system diverges light. For better understanding, the solution is explained with the help of a diagram.