Question

An N-P-N transistor in a common emitter mode is used as a simple voltage amplifier with a collector current of $4mA$. The terminal of a $8V$ battery is connected to the collector through a load resistance ${R_L}$, and to the base through a resistance ${R_B}$. The collector emitter voltage ${V_{CE}} = 4V$, base-emitter voltage ${V_{BE}} = 0.6V$ and base current amplification factor ${\beta _{dc}} = 100$. Calculate the values of ${R_L}$ and ${R_B}$.

Answer 1

Apply Kirchhoff’s voltage law to calculate the resistances in the given circuit. It states that the algebraic sum of all electromotive forces and voltage drops across all the resistors is zero for a given closed loop circuit.
The base current amplification factor in common emitter mode is the ratio of collector current and base current. i.e., ${\beta _{dc}} = \dfrac{{{I_C}}}{{{I_B}}}$.

Complete step by step answer:
Draw the circuit containing a common-emitter mode N-P-N transistor which is used as a voltage amplifier.

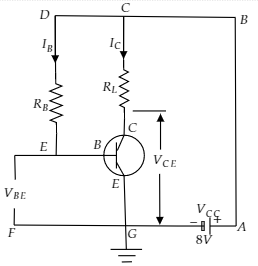
It is given that the potential difference of the battery ${V_{CC}} = 8V$
The collector emitter voltage ${V_{CE}} = 4V$
The collector current ${I_C} = 4mA$
Base-emitter voltage ${V_{BE}} = 0.6V$
Base current amplification factor ${\beta _{dc}} = 100$
Apply the KVL to the loop ABCGA, we got
${I_C}{R_L} + {V_{CE}} = {V_{CC}}$
$\Rightarrow {R_L} = \dfrac{{{V_{CC}} - {V_{CE}}}}{{{I_C}}}$
Substituting all the required values in the above equation
$\Rightarrow {R_L} = \dfrac{{8V - 4V}}{{4 \times {{10}^{ - 3}}A}}$
Further calculate.
$\Rightarrow {R_L} = {10^3}\Omega$
Or ${R_L} = 1K\Omega$
Now we know that ${\beta _{dc}} = \dfrac{{{I_C}}}{{{I_B}}}$
${I_B} = \dfrac{{{I_C}}}{{{\beta _{dc}}}}$
Substitute the value of ${I_C}$ and ${\beta _{dc}}$ in the above formula of ${I_B}$.
${I_B} = \dfrac{{4 \times {{10}^{ - 3}}A}}{{100}}$
Or ${I_B} = 4 \times {10^{ - 5}}A$
Apply the kVL to the loop CDEFGC, we got
${I_B}{R_B} + {V_{BE}} = {V_{CC}}$
Simplify above equation for ${R_B}$.
$\Rightarrow {R_B} = \dfrac{{{V_{CC}} - {V_{BE}}}}{{{I_B}}}$
Substitute all the required values in the above equation for ${R_B}$.
$\Rightarrow {R_B} = \dfrac{{8V - 0.6V}}{{4 \times {{10}^{ - 5}}A}}$
$\Rightarrow {R_B} = 1.85 \times {10^5}\Omega$
Or ${R_B} = 185k\Omega$
The values of ${R_L}$ and ${R_B}$ are $1k\Omega$ and $185k\Omega$ respectively.

Note: It should be noted that the emitter-base junction is forward biased and collector-base is reversed biased. The emitter current is equal to the sum of collector current and base current.