Question
Question: An L-shaped object, made up of thin rods of uniform mass density, is suspended with a string as show...
An L-shaped object, made up of thin rods of uniform mass density, is suspended with a string as shown in figure. If AB=BC , and the angle made by AB with downward vertical is θ , then:
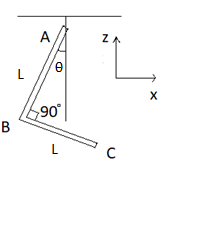
(A) tanθ=32
(B) tanθ=31
(C) tanθ=21
(D) tanθ=231
Solution
to solve this problem we should know about the torque balancing:
Torque: it is the tendency of the body of a force to rotate a body to which it is applied.
Mathematically: τ=rFsinθ .
So to keep a body stable torque should be kept balanced.
Complete step by step solution:
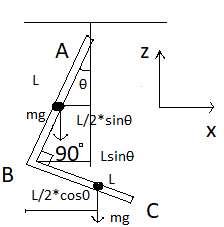
To solve this problem we have to balance torque experienced on two two limbs of the L-shape due to gravitational force.
So first take torque at first limb by gravitational force. By using figure we get,
τ1=mg2Lsinθ
Same for the second limb torque due to gravitational force will be,
τ2=mg(2Lcosθ−Lsinθ)
To keep the torque balance at both points the direction will be reversed to each other.
So, In magnitude both will be equal.
⇒mg(2L+L)sinθ=mg2Lcosθ
⇒mg23Lsinθ=mg2Lcosθ
⇒tanθ=31
From above calculation. We get tanθ=31 .
So, option (b) is the correct option.
Note:
As all rotational motion have an axis of rotation, torque must be defined about a rotational axis. So, a torque is a force applied to a point on an object about the axis of rotation. Torque is an important part of generating power from a car’s engine and transmission of power. For a given force torque can be increased by increasing the radius about which it acts.
