Question

An isosceles triangle with base 24 and legs of 15 is inscribed in a circle. Find the radius.
A.7
B.$12\dfrac{1}{2}$
C.25
D.$25\dfrac{1}{2}$
E.Cannot be determined

Answer 1

We will calculate the radius of the circumcircle by drawing a perpendicular to the base of the triangle, say x, and then from the figure, in triangle ADC, we will use Pythagoras theorem: ${\left( {{\text{hypotenuse}}} \right)^2} = {\left( {{\text{base}}} \right)^2} + {\left( {{\text{perpendicular}}} \right)^2}$to calculate the value of r.

Complete step-by-step answer:
We are given that the base of an isosceles triangle is 24 and its sides are of 15 and it is inscribed in a circle.
Let us draw a perpendicular from the centre of the circle to the base of the triangle.
The figure of this setup:

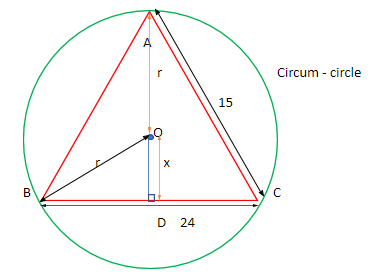
From the figure, we can see that OA is the radius of the circumcircle. Since D is the midpoint of the base BC (ABC being an isosceles triangle), then DC = BD =$\dfrac{{24}}{2}$= 12
Now, using the Pythagoras theorem in triangle ADC, we get
$\Rightarrow$ ${\left( {{\text{hypotenuse}}} \right)^2} = {\left( {{\text{base}}} \right)^2} + {\left( {{\text{perpendicular}}} \right)^2}$= ${\left( {AC} \right)^2} = {\left( {DC} \right)^2} + {\left( {AD} \right)^2}$
Putting their values, we get
$\Rightarrow$ ${\left( {15} \right)^2} = {\left( {12} \right)^2} + {\left( {r + x} \right)^2}$
$\Rightarrow 225 = 144 + {\left( {r + x} \right)^2} \\\ \Rightarrow 225 - 144 = {\left( {r + x} \right)^2} \\\ \Rightarrow 81 = {\left( {r + x} \right)^2} \\\$
$\Rightarrow r + x = 9$ equation (1)
Now, in right triangle ODB, using the Pythagoras theorem, we get
$\Rightarrow O{B^2} = B{D^2} + O{D^2}$
$\Rightarrow {r^2} = {12^2} + {x^2} \\\ \Rightarrow {r^2} - {x^2} = 144 \\\ \Rightarrow \left( {r + x} \right)\left( {r - x} \right) = 144 \\\$
Substituting the value of r + x, we get
$\Rightarrow 9\left( {r - x} \right) = 144$
$\Rightarrow \left( {r - x} \right) = 16$ equation (2)
Now, adding both the equations (1) and (2), we get
$\Rightarrow \left( {r + x} \right) + \left( {r - x} \right) = 16 + 9 \\\ \Rightarrow 2r = 25 \\\ \Rightarrow r = \dfrac{{25}}{2} = 12\dfrac{1}{2} \\\$
We obtained the value of the radius of the circumcircle as $12\dfrac{1}{2}$ .
Hence, option(B) is correct.

Note: In this question, you may get confused with the method used because we have to construct a perpendicular in order to obtain the value of the radius of the circle using the Pythagoras theorem twice. You can also solve this question by putting the value of x in terms of r from (1) in equation (2).