Question

An isosceles prism of angle $A = 30^\circ$ has one of its surfaces silvered. Light rays falling at an angle of incidence $60^\circ$ on the other surface retrace their path after reflection from the silvered surface. The refractive index of prism material is

A. 1.414
B. 1.5
C. 1.732
D. 1.866

Answer 1

Hint: Refractive index can be calculated by taking the ratio of sines of angles of incidence and angle of refraction. We are given the angle of incidence and we need to calculate angle of refraction using available information.

Complete step-by-step answer:
The phenomenon of bending of light when it travels from one medium to another is called refraction.
Refraction is governed by two laws of refraction given below:
1. The incident and refracted light ray and the normal drawn perpendicular at the point of incidence, all lie in the same vertical plane.
2. If we take ratio of the sine of the angle of incidence to the sine of the angle of refraction, we get a quantity called the refractive index which decides the amount of refraction of light and is given as
$\mu = \dfrac{{\sin i}}{{\sin r}}$
Where $\mu$ is called the refractive index, i is the angle of incidence and r is the angle of refraction.
We are given an isosceles prism with angle of prism given as:
$A = 30^\circ$
One of the sides of the prism is polished as can be seen in the figure below. The polished side will act as a mirror now and reflect the light rays incident on it.
The question says that when the light ray enters the prism, it gets reflected from the polished surface such that it retraces its original path. This is possible only when the light ray strikes the mirror at angle of 90$^\circ$.

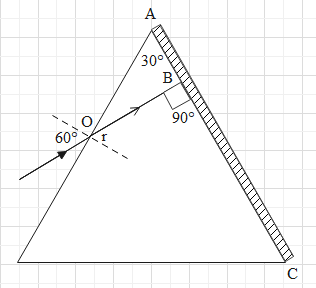
Now we just need to find the angle of refraction r which can be done in the following way. Consider the $\Delta AOB$, we can use the property that exterior angle of a triangle is equal to the sum of the interior opposite angle and can write the following relation:
$\angle OBC = \angle OAB + \angle AOB \\\ \Rightarrow 90 = 30 + \angle AOB \\\ \Rightarrow \angle AOB = 90 - 30 = 60^\circ {\text{ }}...{\text{(i)}} \\\$
Now as when know that normal makes an angle of 90$^\circ$ with the face of the prism, we can write that
$\angle r + \angle AOB = 90^\circ \\\ \Rightarrow \angle r = 90 - \angle AOB \\\$
Using equation (i), we get
$\angle r = 90 - 60 = 30^\circ \\\ \therefore \mu = \dfrac{{\sin i}}{{\sin r}} \\\$
Substituting the known values, we get
$\mu = \dfrac{{\sin 60^\circ }}{{\sin 30^\circ }} = \dfrac{{\dfrac{{\sqrt 3 }}{2}}}{{\dfrac{1}{2}}} = \sqrt 3 = 1.732$
Hence, the correct answer is option C.

Note: The light ray incident on the mirror follows the laws of reflection which state that angle of incidence is equal to the angle of reflection and the incident ray, reflected ray and normal at the point of incidence lie in the same plane. Since the angle of incidence on a mirror is zero in our case, the angle of reflection is also zero and the light ray retraces its path.