Question

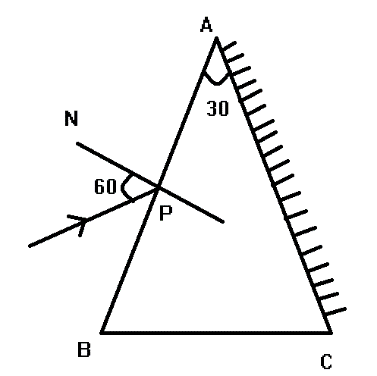
An isosceles prism of angle $A = {30^\circ }$ has one of its surfaces silvered. Light rays falling at an angle of incidence ${60^\circ }$ on the other surface retrace their path after reflection from the silvered surface. The refractive index of prism material is

(A) $1.414$
(B) $1.5$
(C) $1.732$
(D) $1.866$

Answer 1

Hint Here in this question we start by using Snell’s law which describes the relationship between the angle of incidence and angle of refraction. By using this relation we will find the refractive index of the given prism by using the relationship between the angle of incidence and angle of refraction.
Formula used
$\Rightarrow \frac{{{\eta _2}}}{{{\eta _1}}} = \frac{{\sin {\vartheta _i}}}{{\sin {\vartheta _r}}}$
$\Rightarrow \angle PDC = \angle DAC + \angle APD$

Complete Step by step solution

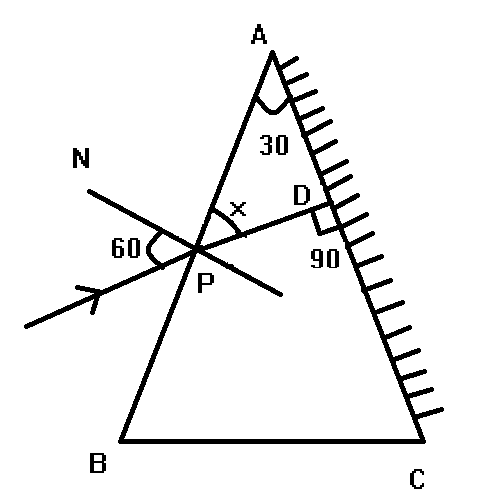
Here from the figure, we can observe that angle of incidence is given which is {60^^\circ } and also given that the angle of the prism is {30^^\circ } . Starting with Snell’s law which states that
$\Rightarrow {\eta _1}\sin {\vartheta _i} = {\eta _2}\sin {\vartheta _r}$
$\Rightarrow \frac{{{\eta _2}}}{{{\eta _1}}} = \frac{{\sin {\vartheta _i}}}{{\sin {\vartheta _r}}}$
Here, ${\eta _1} = 1$(for air the refractive index is $1$ )
And ${\eta _2}$ is the refractive index of the prism
Hence we get
$\Rightarrow {\eta _2} = \frac{{\sin {\vartheta _i}}}{{\sin {\vartheta _r}}}$ -------- equation $(1)$
$\therefore {\vartheta _i} = {\text{ }}60^\circ$(Angle of incidence) given so at first we have to find the angle of refraction ${\vartheta _r}$ .
Now from the diagram, we can see that in the triangle $\Delta APD$ from the exterior angle property which states that the exterior angle of a triangle is equal to the sum of opposite interior angles of the triangle. So
$\Rightarrow \angle PDC = \angle DAC + \angle APD$
$\therefore \angle APD = \angle DAC - \angle PDC$
Substituting the values in the above equation,
$\Rightarrow x = {90^\circ } - {30^\circ }$
$\therefore x = {60^\circ }$
Now from the above value of $x$ , we can obtain the angle of refraction ${\vartheta _r}$
$\Rightarrow {\vartheta _r} = {90^\circ } - x$
$\therefore {\vartheta _r} = {90^\circ } - {60^\circ } = {30^\circ }$
Now putting the value of ${\vartheta _r}$ in the equation $(1)$ we get the refractive index of the prism ${\eta _2}$
$\Rightarrow {\eta _2} = \frac{{\sin {{60}^\circ }}}{{\sin {{30}^\circ }}}$
$\therefore {\eta _2} = \sqrt 3 = 1.732$
Therefore the refractive index of prism material is ${\eta _2} = 1.732$ .

So the option (C) is the correct answer.

Note Here the above question is solved by following Snell’s law which is also known as the law of refraction which states the relationship between the angle of incidence, angle of refraction, and the absolute refractive index of the respective mediums.