Solveeit Logo
Login

Question

Question: An isosceles prism of angle \({120^o}\) has a refractive index 1.44. Two parallel monochromatic rays...

An isosceles prism of angle 120o{120^o} has a refractive index 1.44. Two parallel monochromatic rays enter the prism parallel to each other in air as shown in fig. The rays emerging from the opposite faces:

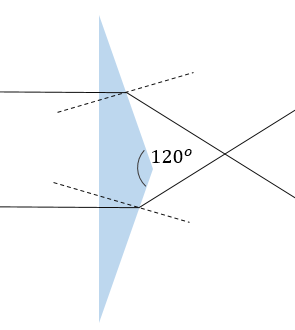
A. Are parallel to each other
B. Are diverging
C. Make an angle of 2sin−1(0.72)2si{n^{ - 1}}(0.72) with each other
D. Make an angle of 2sin−1(0.72)−30o2si{n^{ - 1}}(0.72) - {30^o} with each other

Explanation

Solution

Hint: We can first find the angle of incidence for the rays coming out of the prism. Then Snell’s Law can be used to calculate the angle of refraction and then the angle of deviation. The angle between the parallel rays after refraction would be the sum of deviations of each ray.

Complete step by step answer:
We are given an isosceles prism into which the rays are entering normally. We know that for isosceles triangles, two angles are equal and the sides opposite to these angles are also equal. Also, a perpendicular drawn from the midpoint of the base bisects the angle opposite to it.

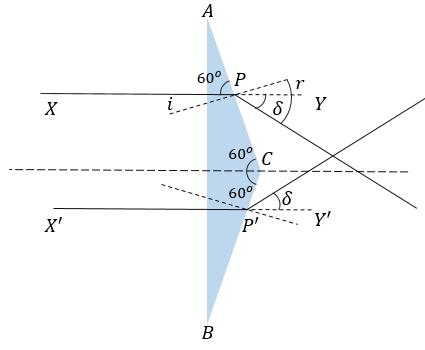
So we can see from the diagram that ∠CPY=60o=∠XPA\angle CPY = {60^o} = \angle XPA and so is ∠CP′Y′\angle CP'Y'
If ii is the angle of incidence, then we can see i=90−∠XPA=90−60=30oi = 90 - \angle XPA = 90 - 60 = {30^o}
We can now use Snell's law to find the angle of refraction.
sinisinr=n2n1\dfrac{{sini}}{{sinr}} = \dfrac{{{n_2}}}{{{n_1}}} where n2{n_2} and n1{n_1} are the refractive indices of final and initial medium respectively.
Let's apply this to ray XP.
sin30sinr=11.44\dfrac{{sin30}}{{sinr}} = \dfrac{1}{{1.44}}
sinr=1.442sinr = \dfrac{{1.44}}{2}
r=sin⁡−1(0.72)r = {\sin ^{ - 1}}(0.72)

Now, we can find the angle made by the ray with horizontal as δ=r−i=sin⁡−1(0.72)−30\delta = r - i = {\sin ^{ - 1}}(0.72) - 30
Now, the total angle between the emerging rays is the sum of deviation ( δ\delta ) of the two rays. Since both rays are refracted similarly, the total deviation would be 2δ=2(sin⁡−1(0.72)−30)2\delta = 2\left( {{{\sin }^{ - 1}}(0.72) - 30} \right)
This is the required answer and the corresponding option is D.

Note: The angle of a prism is usually the angle between the plane through which light ray enters and the plane through which it exits. Here the angle mentioned is not the angle of prism and should not be considered as AA in any equation.