Question

An iron bar of length L, cross-section area A and Young’s modulus Y is pulled by a force F from ends so as to produce an elongation l. Which of the following statements is correct?
$\left( a \right)1\propto \dfrac{1}{L}$
$\left( b \right)1\propto A$
$\left( c \right)1\propto \dfrac{1}{A}$
$\left( d \right)1\propto Y$

Answer 1

As the question includes Young’s modulus so, we will first use stress and strain for an object and after taking the ratio of stress to the strain we will get the formula for Young’s Modulus. After getting the required equation we will take all terms to the right side of the equation leaving only 1 on the left side. This will help in checking proportionality.

Formula used:
$Stress=\dfrac{F}{A},Strain=\dfrac{{{L}_{\left( new \right)}}-{{L}_{\left( old \right)}}}{{{L}_{\left( old \right)}}}$and $Y=\dfrac{F{{L}_{old}}}{A\left( {{L}_{new}}-{{L}_{old}} \right)}$. Here, F is the force and ${{L}_{\left( old \right)}}$ is the original length of the object and ${{L}_{\left( new \right)}}$ is the new length of an object. A is called the cross-sectional area and $Y$ is called Young’s modulus.

Complete step by step answer:
Young’s Modulus: Young’s modulus is a modulus of elasticity (whether compressing or elongating) of any material which can remain unaffected by the changes caused in the length of the material. This gives the elasticity of any substance which remains unbreakable after creating slight tension in its length by elongating it or compressing it. For its numerical value we will suppose that there is an object which is of the form of a cube. Let us consider that forces are applied on the substance by elongating its length by its two end points by considering the two forces as ${{F}_{1}}$ and ${{F}_{2}}$ which may or may not be equal. This can be understood by the following diagram.

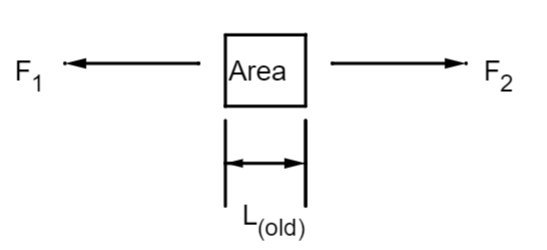
Here, ${{L}_{\left( old \right)}}$ is the original length of the object. As a result of the tension created by the forces the object will change its length from its original position to its new length as ${{L}_{\left( new \right)}}$. This can be seen in the below mentioned diagram.

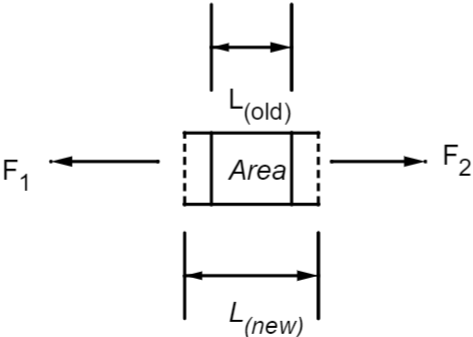
The stress created here can be found out by the ratio of the force F which is up to an extent which can be stretched without breaking to the cross-sectional area represented as Area or A. This is numerically written as $Stress=\dfrac{F}{A}$. Due to the elongation of the object the strain on the object is calculated as $Strain=\dfrac{{{L}_{\left( new \right)}}-{{L}_{\left( old \right)}}}{{{L}_{\left( old \right)}}}$. Now, the ratio of stress to the strain is known as the Young’s Modulus. We can also numerically form an equation of the Young’s Modulus which can be written as,
$Y=\dfrac{Stress}{Strain}$
$\Rightarrow Y=\dfrac{\dfrac{F}{A}}{\dfrac{{{L}_{\left( new \right)}}-{{L}_{\left( old \right)}}}{{{L}_{\left( old \right)}}}}$
If we let that $\dfrac{\dfrac{F}{A}}{\dfrac{{{L}_{\left( new \right)}}-{{L}_{\left( old \right)}}}{{{L}_{\left( old \right)}}}}=\dfrac{\dfrac{F}{A}}{\dfrac{\Delta l}{l}}$ so, we get $Y=\dfrac{\dfrac{F}{A}}{\dfrac{\Delta l}{l}}$ which can also be written as $1=\dfrac{\dfrac{F}{A}}{Y\left( \dfrac{\Delta l}{l} \right)}$ or $1=\dfrac{F}{AY}\left( \dfrac{l}{\Delta l} \right)$. As length is L given to us so, $\dfrac{l}{\Delta l}=L$ thus, $1=\dfrac{FL}{AY}$.
Now, we get $1\propto L,1\propto \dfrac{1}{A},1\propto \dfrac{1}{Y}$ conditions as a result of outcome.
Hence, the correct option is $\left( c \right)1\propto \dfrac{1}{A}$.

Note:
To solve this question we need to follow below written points.
(1) The formula and definition of stress: $Stress=\dfrac{F}{A}$.
(2) The formula and definition of strain: $Strain=\dfrac{{{L}_{\left( new \right)}}-{{L}_{\left( old \right)}}}{{{L}_{\left( old \right)}}}$.
(3) The formula and definition of Young’s Modulus: $Y=\dfrac{F{{L}_{old}}}{A\left( {{L}_{new}}-{{L}_{old}} \right)}$.
(4) The elongation is directly proportional to length and inversely proportional to area of cross section.