Question

An inverted conical container has a diameter of 42 inches and a depth of 15 inches. If water is flowing out of the vertex of the container at a rate of $35\pi \text{ i}{{\text{n}}^{3}}/\text{sec}$ how fast is the depth of the water dropping when the height is 5 inches.

Answer 1

Firstly, we have to find the radius from the given diameter. Then, take the ratio of the radius and the height and find radius in terms of height. Substitute this value of radius in the formula for volume of the container which is given by $V=\dfrac{1}{3}\pi {{r}^{2}}h$ . Differentiate the resultant volume with respect to t and substitute the given value $\dfrac{dV}{dt}=-35\pi \text{ i}{{\text{n}}^{3}}/\text{sec}$ and the height which will be 5 inches. Find the value of $\dfrac{dh}{dt}$ .

Complete step by step answer:
We are given that the diameter of the cone is 42 inches. Therefore, the radius can be found by dividing the diameter by 2.
$\begin{aligned} & \Rightarrow r=\dfrac{d}{2} \\\ & \Rightarrow r=\dfrac{42}{2} \\\ & \Rightarrow r=21\text{ in} \\\ \end{aligned}$

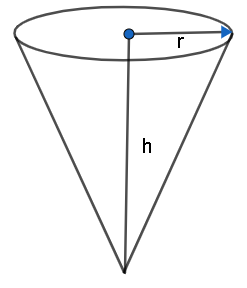
Let us find the volume of the container. We know that volume of a cone is given by
$V=\dfrac{1}{3}\pi {{r}^{2}}h$
Where r is the radius and h is the height of the cone. We are given that the depth of the cone, that is, height is 15 inches. Let us take the ratio of radius and height.
$\begin{aligned} & \Rightarrow \dfrac{r}{h}=\dfrac{21}{15} \\\ & \Rightarrow \dfrac{r}{h}=\dfrac{7}{5} \\\ \end{aligned}$
Let us find r in terms of h.
$\Rightarrow r=\dfrac{7}{5}h$
Now, we have to substitute the above value in the volume of the cone.
$\Rightarrow V=\dfrac{1}{3}\pi {{\left( \dfrac{7}{5}h \right)}^{2}}h$
$\Rightarrow V=\dfrac{49}{75}\pi {{h}^{3}}...\left( i \right)$
We are given that the water is flowing out of the vertex of the container at a rate of $35\pi \text{ i}{{\text{n}}^{3}}/\text{sec}$ , that is,
$\Rightarrow \dfrac{dV}{dt}=-35\pi \text{ i}{{\text{n}}^{3}}/\text{sec}$
Let us differentiate the equation (i) with respect to t.

$\Rightarrow \dfrac{dV}{dt}=\dfrac{49}{75}\pi \times 3{{h}^{2}}\times \dfrac{dh}{dt}$
We have to find the rate at which the depth of the water is dropping when the height is 5 inches.

& \Rightarrow -35\pi =\dfrac{49}{25}\pi \times {{\left( 5 \right)}^{2}}\times \dfrac{dh}{dt} \\\ & \Rightarrow -35\pi =49\pi \dfrac{dh}{dt} \\\ & \Rightarrow -35\require{cancel}\cancel{\pi }=49\require{cancel}\cancel{\pi }\dfrac{dh}{dt} \\\ & \Rightarrow \dfrac{dh}{dt}=-\dfrac{35}{49} \\\ & \Rightarrow \dfrac{dh}{dt}=-\dfrac{5}{7} \\\ & \Rightarrow \dfrac{dh}{dt}=-0.714\text{ in/sec} \\\ \end{aligned}$$ Therefore, the rate at which the depth of the water is dropping when the height is 5 inches is 0.714 in/s. **Note:** Students must be thorough with the formulas of 2D and 3D shapes. They have a chance of making a mistake by writing the volume of the cone as $V=\dfrac{1}{3}\pi {{r}^{2}}l$ , where l is the slant height. They must never forget to write the units at the end of each calculation. Students must never miss inserting a negative sign in $\dfrac{dV}{dt}$ since the water is leaving the container.