Question
Question: An inverted cone has a depth of 40 cm and a base of radius 5 cm. Water is poured into it at a rate o...
An inverted cone has a depth of 40 cm and a base of radius 5 cm. Water is poured into it at a rate of 1.5 cubic centimetres per minute. Find the rate at which the level of water in the cone is rising when the depth is 4 cm.
Solution
Hint: In this question draw a diagram to get a visual representation of the problem. After that use the basic proportionality theorem to find the relation between the two triangles formed. Use this relation in the formula of volume and differentiate the obtained equation so that you obtain the value of dtdh which will be the required answer.
Complete step-by-step answer:
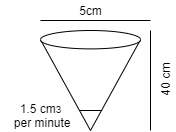 We know that volume of a cone = 31πr2h equation (1)
We know that volume of a cone = 31πr2h equation (1)
Let the height of the water level be h and radius be r. So according to B.P.T., 405=hr …. equation (2) One solving equation (1) we get, r =8h … equation (3)
Putting values of equation (3) in equation (1) we get, V = 31π(8h)2h … equation (4) So, differentiating both sides on equation (4) we get dtdv=dtd(192πh3) According to question , we are given the rate at which the level of water in the cone is rising dtdv=1.5 So, 1.5 =dtd(192πh3)
64πh2dtdh=1.5 dtdh=πh296
Now, when h = 4
dtdh=π6cm/s
Note: In the above question we used a term differentiation that has many applications in real life. One of its very important applications of derivatives is found in its use in the calculation of the rate of change of quantity in relation to other quantities.
