Question

An insulating rod of length ‘l’ carries a charge ‘q’ distributed on it. The rod is pivoted at its midpoint and is rotated at a frequency ‘f’ about a fixed axis perpendicular to the rod and passing through the pivot. The magnetic moment of the rod system is.

Answer 1

Considering a small element at a distance xx of small width dx.dx.
Magnetic moment of the small element is- $dm = 2\pi (lqdx)\omega \pi r^2$.The magnetic moment of the whole rod can be found by integrating that value over the whole length of the rod.

Complete answer:
Let a rod be given and is fixed at its mid-point. So here, we have to find the magnetic moment of the rod system.
Let's go to ‘x’ distance and take an element named ‘dx’.

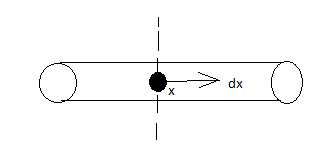
Then dm $=$ idA
In l length charge is q; I length charge is

\\\ \dfrac{{q\pi f{l^2}}}{{12}} \\\ $$; dx length charge is $$\dfrac{q}{l} \times dx$$. $$\int { = qf} $$

\therefore dm = idA \\
= \dfrac{q}{l}dx \\

Since, $$i = \dfrac{q}{T}$$ we can write this in frequency terms as $$l = qf$$ Then, if the area is $$\pi {r^2}$$ and is rotating along with the ‘x’ radius hence the equation will be $$dm = \dfrac{q}{l}dxf{\pi ^2}$$. Now here we got the magnetic moment due to the small element. If we have to find the entire magnetic moment then we will integrated the dm function and the equation will now become as : $${\int {dm = \int {\dfrac{q}{{{l_{_{\dfrac{{ - l}}{2}}}}}}} } ^{\dfrac{l}{2}}} \times f\pi {x^2}dx$$ $$m = \dfrac{q}{l} \times \pi f{[\dfrac{{{x^3}}}{3}]^{\dfrac{l}{2}}}_{\dfrac{{ - l}}{2}}$$ After this we get,

= \dfrac{{q\pi f}}{l} \times [\dfrac{{{l^3}}}{{24}} - (\dfrac{{ - {l^{}}}}{{24}})] \\
= \dfrac{{q\pi f}}{l}(\dfrac{{2{l^3}}}{{24}}) \\
= \dfrac{{q\pi f{l^2}}}{{12}} \\

$$Hence, the correct answer is$$

\\\  

\dfrac{{q\pi f{l^2}}}{{12}} \\

**Note:** The magnetic moment is the strength and orientation of a magnet or any other object that produces a magnetic field. The rod sweeps a circle of radius $$\dfrac{1}{2}$$.