Question

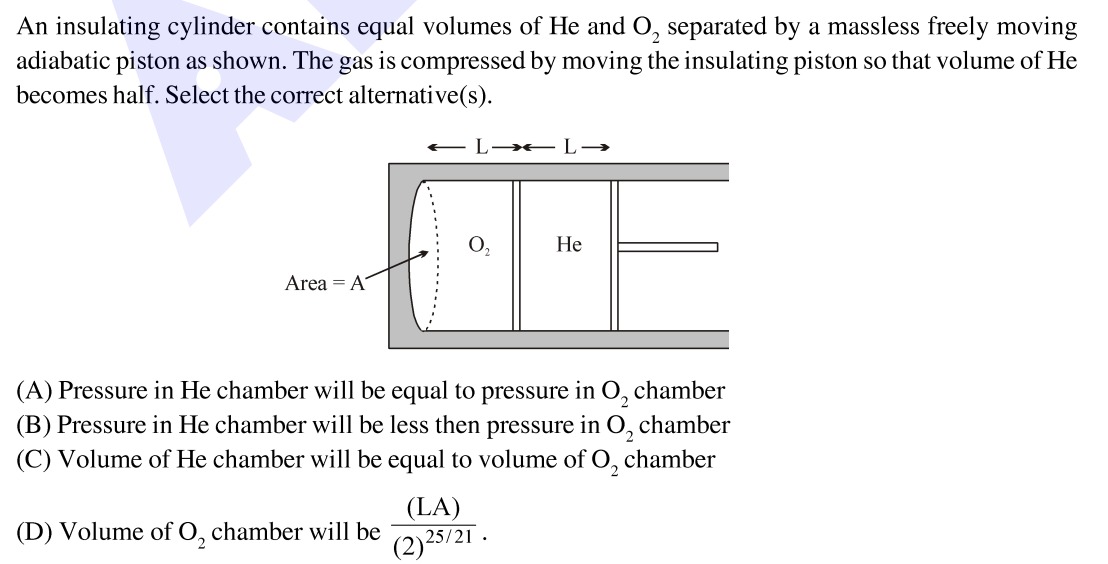
An insulating cylinder contains equal volumes of He and O₂ separated by a massless freely moving adiabatic piston as shown. The gas is compressed by moving the insulating piston so that volume of He becomes half. Select the correct alternative(s).

• A. Pressure in He chamber will be equal to pressure in O₂ chamber
• B. Pressure in He chamber will be less then pressure in O₂ chamber
• C. Volume of He chamber will be equal to volume of O₂ chamber
• D. Volume of O₂ chamber will be $\frac{(LA)}{(2)^{25/21}}$

Answer 1

Answer: (A), (D)

A, D

Answer 2

Let the initial volume of He and O₂ be $V_0$. From the diagram, if the area of the piston is $A$ and the initial length of each chamber is $L$, then $V_0 = LA$.

Initially, the piston separating He and O₂ is massless and freely moving, so the pressure in both chambers is equal: $P_{He,1} = P_{O₂,1} = P_1$.

The gas is compressed adiabatically such that the final volume of He is $V_{He,2} = \frac{1}{2} V_{He,1} = \frac{V_0}{2}$.

Since the piston separating He and O₂ is adiabatic and freely moving, the pressure in both chambers in the final state is also equal: $P_{He,2} = P_{O₂,2} = P_2$.

The compression process for each gas is adiabatic.

For He (monatomic gas, $\gamma_{He} = 5/3$):

$P_{He,1} V_{He,1}^{\gamma_{He}} = P_{He,2} V_{He,2}^{\gamma_{He}}$

$P_1 V_0^{5/3} = P_2 (\frac{V_0}{2})^{5/3}$

$P_2 = P_1 \left(\frac{V_0}{V_0/2}\right)^{5/3} = P_1 (2)^{5/3}$.

For O₂ (diatomic gas, $\gamma_{O₂} = 7/5$):

$P_{O₂,1} V_{O₂,1}^{\gamma_{O₂}} = P_{O₂,2} V_{O₂,2}^{\gamma_{O₂}}$

$P_1 V_0^{7/5} = P_2 V_{O₂,2}^{7/5}$

Substituting $P_2 = P_1 (2)^{5/3}$:

$P_1 V_0^{7/5} = P_1 (2)^{5/3} V_{O₂,2}^{7/5}$

$V_0^{7/5} = (2)^{5/3} V_{O₂,2}^{7/5}$

$\frac{V_0^{7/5}}{V_{O₂,2}^{7/5}} = 2^{5/3}$

$\left(\frac{V_0}{V_{O₂,2}}\right)^{7/5} = 2^{5/3}$

$\frac{V_0}{V_{O₂,2}} = (2^{5/3})^{5/7} = 2^{(5/3) \times (5/7)} = 2^{25/21}$.

$V_{O₂,2} = \frac{V_0}{2^{25/21}}$.

Now let's check the options:

(A) Pressure in He chamber will be equal to pressure in O₂ chamber. This is correct because the separating piston is massless and freely moving.

(B) Pressure in He chamber will be less than pressure in O₂ chamber. This is incorrect.

(C) Volume of He chamber will be equal to volume of O₂ chamber. $V_{He,2} = V_0/2$. $V_{O₂,2} = V_0/2^{25/21}$. Since $25/21 > 1$, $2^{25/21} > 2$. Thus $1/2^{25/21} < 1/2$. So $V_{O₂,2} < V_{He,2}$. This is incorrect.

(D) Volume of O₂ chamber will be $\frac{(LA)}{(2)^{25/21}}$. Since $V_0 = LA$, we have $V_{O₂,2} = \frac{LA}{2^{25/21}}$. This is correct.