Question

An insect jumps from ball $A$ onto ball $B$, which are suspended from inextensible light strings each of length $L=8\text{ cm}$. The mass of each ball and insect is the same. What should be the minimum relative velocity (in $m{{s}^{-1}}$) of jump of insect w.r.t. ball $A$, if both the balls manage to complete the full circle?

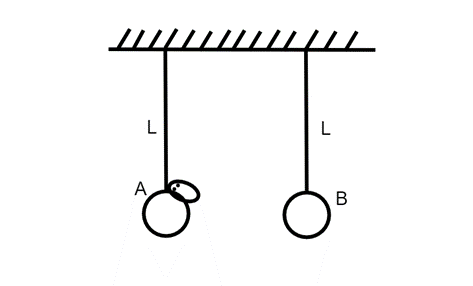
A. $9$
B. $8$
C. $10$
D. $20$

Answer 1

To solve this problem we will use the concept of conservation of linear momentum because no external force acts on the system. We have considered the insect and both the balls as a system in this case whose linear momentum will be conserved. Also, we need to recall the velocity required by an object to complete a circle when it travels in a circular motion.

Complete step-by-step answer:
Let us assume that the insect jumps from ball $A$ onto ball $B$ with a velocity $u$ and the mass of each ball and insect be $m$. Since, no external force is applied on the system, hence the linear momentum of the system will be conserved. If the insect jumps from ball $A$ onto ball $B$ with a velocity $u$ then it will impart the same velocity $u$ on the ball $A$ in the opposite direction. On conserving the momentum considering that the system was initially at rest, we get:
$\begin{aligned} & 0=-mu+2mv \\\ & \Rightarrow 2mv=mu \\\ & \Rightarrow 2v=u \\\ & \Rightarrow v=\dfrac{u}{2} \\\ \end{aligned}$
Thus, ball $B$ will have a velocity of $\dfrac{u}{2}$ and if the balls have to complete a full circle, then the ball with lower velocity must at least fulfill the condition for completing full circle. To complete full circle:
$\begin{aligned} & \dfrac{u}{2}=\sqrt{5gl} \\\ & \Rightarrow \dfrac{u}{2}=\sqrt{5\times 10\times 0.08} \\\ & \Rightarrow \dfrac{u}{2}=2 \\\ & \Rightarrow u=4 \\\ \end{aligned}$
The minimum relative velocity will be:
$\begin{aligned} & {{u}_{rel}}={{u}_{2}}-{{u}_{1}} \\\ & \Rightarrow {{u}_{rel}}=u-\left( -u \right) \\\ & \Rightarrow {{u}_{rel}}=u+u \\\ & \Rightarrow {{u}_{rel}}=2u \\\ & \Rightarrow {{u}_{rel}}=2\times 4 \\\ & \therefore {{u}_{rel}}=8\text{ m}{{\text{s}}^{-1}} \\\ \end{aligned}$

So, the correct answer is “Option B”.

Note: We applied the condition for an object to complete a full circle only on the ball with a lower velocity i.e., ball $B$ because the other ball has a higher velocity and can definitely complete a full circle if the ball with a lower velocity can do so. Our solution would have been incorrect if we used the condition for ball $A$.