Question
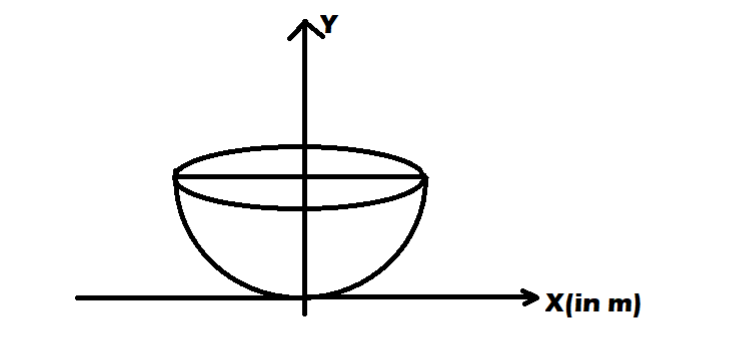
Question: An insect is crawling on a parabolic bowl \((y = {x^2})\) as shown in figure. Find Out the height of...
An insect is crawling on a parabolic bowl (y=x2) as shown in figure. Find Out the height of the point where the insect starts skidding (μ=31)
Solution
Hint In these kinds of situations the first thing important is to notice the given problem statement. Specially this is a question regarding some manipulation. First we just have to sort what we got and then we just have to interpret the missing quantities for the equation. In this question we will get the answer simply by putting the values in the equation of force.
Complete step-by-step answer:
Here, according to the figure the forces are balanced in a manner :
N=mgcosα
And the frictional force is given by:
f=mgsinα
Therefore by interpreting and equating both the above questions we get:
tanα=Nf
And it is also equal to tanα=μ . So we get:
μ=31 tanα=31 or, cotα=3
Note Most important thing here is to notice the given values, then we can easily derive the missing quantities. Apart from that it is necessary to observe what process is straight and easy to find the rest values and then we can execute the formulas. In these types of questions interpreting the correct formula to be used is necessary unless it will get twisted.
