Question
Question: An infinitely long uniform line charge distribution of charge of per unit length \(\lambda \)lies pa...
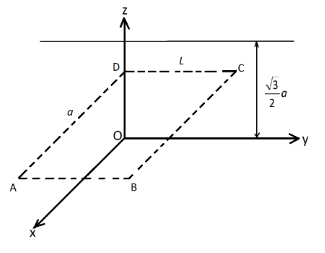
An infinitely long uniform line charge distribution of charge of per unit length λlies parallel to the y-axis in the y-z plane at z=23a. If the magnitude of the flux of the electric field through the rectangular surface ABCD lying in the x-y plane with its center at the origin is nε0λL (ε0 = permittivity of the free space), then the value of n is:
Solution
The above problem can be solved by using the Gauss’s law of electric flux. The gauss’s law states that the total flux inside a closed surface is equal to the ε01 times of the charge enclosed in the closed surface. To solve the above problem we have to find the angle subtended by the corner A of the rectangular surface ABCD to the intersection point at z axis. This gives the idea about the shape of the closed surface then we can apply Gauss's law to find the value of the n.
Complete step by step answer:
Given; The length of the rectangular surface is AD=a.
The width of the rectangular surface is L.
The distance of the rectangular surface from the z axis is z=23a.
The magnitude of the flux of the electric field through the rectangular surface is ϕ=nε0λL.
The expression to find the angle subtended by the corner A of the rectangular surface at the intersection point at z axis is given as:
tanα=zAD
Substitute 2a for AD and 23afor z in the above expression to find the angle subtended by the rectangular surface.
tanα=23a2a
⇒tanα=31
⇒α=60∘
The expression to calculate the flux through the rectangular surface is given as,
ϕ=6ε0λL.......(1)
The expression (1) consists of 6 in the denominator because the rectangular surface is one face from the six faces of cuboid and flux pass from the rectangular surface is one sixth of the total flux in the cuboid.
Substitute nε0λL for ϕ in the expression (1) to find the value of n.
6ε0λL=nε0λL
∴n=6
Thus, the value of n is 6.
Note: The Gauss’s law is applicable only for closed surface and flux outside the closed surface becomes zero. The closed surface is called the Gaussian surface. The electric flux passes through each surface of the cuboid is the same because the charge is placed at the center of the cuboid.
