Question
Question: An infinitely long current carrying wire and a small current carrying loop are in the plane of the p...
An infinitely long current carrying wire and a small current carrying loop are in the plane of the paper as shown. The radius of the loop is a and distance of its centre from the wire is (d≫a). If the loop applies a force F on the wire then:
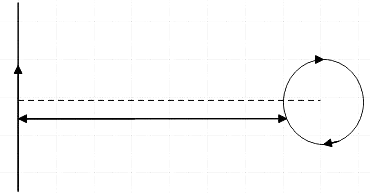
A.F∝(d3a2)
B.F∝(da)
C.F∝(da)2
D.F=0
Solution
First of all you should understand that the loop here acts as a magnetic dipole. Now you could recall the expression for force due to this loop. Then you could find the magnetic moment due to it as well as the magnetic field due to the infinite wire and substitute in that expression. Thereby, you could easily find the relation.
Formula used:
Force as a gradient of magnetic field,
F=m.∇B
Magnetic moment,
m=NIA
Magnetic field at distance x,
B=2πxμ0I
Complete answer:
In the question, we are given a long current carrying wire along with a small current carrying loop kept on the same plane. The radius of this loop is given as a and the distance of separation of the wire with the centre of the loop given as d. We are also told that d≫a. We are asked to find the relation of the force with a and d.
Here the circular loop is acting as a magnetic dipole and we know that the force due to magnetic dipole is given by,
F=m.∇B
Where, m is the magnetic moment of the dipole and B is the magnetic field due to the current carrying wire at the point at which the loop is kept.
Since we are dealing with one dimension, we could rewrite the equation as,
F=m.dxdB………………………………….. (1)
We know that magnetic field due to current carrying wire at a distance x is given by,
B=2πxμ0I ……………………………………… (2)
We know that magnetic moment m due the given loop will be,
m=NIA
But N=1 and A=πa2
⇒m=Iπa2 ………………………………. (3)
Substituting (2) and (3) in (1), we get,
F=(Iπa2)dxd(2πxμ0I)
⇒F=(Iπa2)(−2πx2μ0I)
But x here is given as d, so,
F=−2d2μ0I2a2
Therefore, we found that the force applied by the loop F,
F∝d2a2
Hence, option C is found to be the correct answer.
Note:
We haven’t substituted d for x earlier so as to avoid confusion during differentiation. Also, gradient gives the change of a quantity per unit distance. The negative sign here says that the force exerted is repulsive force. μ0 here is the absolute permeability.
