Question
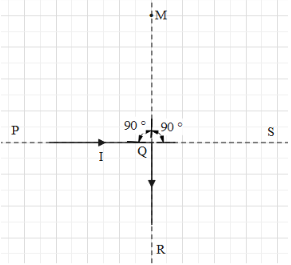
Question: An infinitely long conductor PQR is bent to form a right angle as shown in figure. A current I flows...
An infinitely long conductor PQR is bent to form a right angle as shown in figure. A current I flows through PQR. The magnetic field due to this current carrying conductor at the point M is B1. Now, another infinitely long straight conductor QS, is connected at Q so that the current is 2I in QR as well as in QS, the current in PQ remaining unchanged. The magnetic field at M is now B2. The ratio B2B1 is given by
A. 21
B. 1
C. 32
D. 2
Solution
Use the formula for the magnitude of the magnetic field at a point P due to a straight current carrying conductor and the right hand thumb rule to find the direction of the magnetic field. With these find the magnetic field in both the case and then calculate the ratio of both.
Formula used:
B=4πdμ0I(sinθ1+sinθ2)
where μ0 is the permeability of free space, I is the current in the conductor and θ1, θ2 are the angles .
Complete step by step answer:
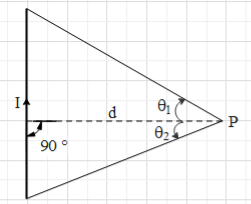
Consider a straight current carrying conduction of length l. The magnitude of the magnetic field at a point P, which is at a perpendicular d from the conductor as shown in the figure is given as B=4πdμ0I(sinθ1+sinθ2),
where μ0 is the permeability of free space, I is the current in the conductor and θ1, θ2 are the angles as shown in the figure.
The direction of the magnetic field is given by the right hand thumb rule.In the first case, the magnetic field at point M due the current in QR is zero since it passes through the axis of QR. The magnetic field at the same point due to current in PQ is B1=4πdμ0I(sin(0)+sin90∘).
(since the conductor is infinitely long, θ2≈90∘).
And sin90∘=1, sin0∘=0.
B1=4πdμ0I …. (i).
From the right hand thumb rule, the direction of B1 is outwards the plane.
In the second case too, the magnetic field at point M due to QR is zero. The magnetic field at the same point due to the current in PQ is BPQ=4πdμ0I.The magnetic field due to the current in QS is,
BQS=4πdμ0(2I)(sin90∘+sin(0)) ⇒BQS=4πdμ0(2I) ⇒BQS=8πdμ0I.
From the right hand thumb rule, the direction of both BPQ and BQS are parallel and outwards the plane.This means that the net magnetic field due to the set up is B2=BPQ+BQS.
⇒B2=4πdμ0I+8πdμ0I.
⇒B2=8πd3μ0I …. (ii).
Now divide (i) by (ii).
⇒B2B1=8πd3μ0I4πdμ0I ∴B2B1=32.
With this we found the value of the ratio.
Hence, the correct option is C.
Note: In the formula for the magnitude of magnetic field that we discussed above, we see that the magnetic field due to PQ and QS is directly proportional to current because all the other factors are the same for both. Therefore, this means that in the second case BQS=2BPQ, since the current in QS is half of the current in PQ.
⇒B2=BPQ+2BPQ ⇒B2=23BPQ.
And in the first case B1=BPQ.
When we divide both, we get that B2B1=23BPQBPQ
⇒B2B1=32.
