Question
Question: An infinitely long conductor carrying the current \(i\) with a semiconductor loop in the \(x - y\) p...
An infinitely long conductor carrying the current i with a semiconductor loop in the x−y plane and two straight parts. One parallel to x axis and another coinciding with z axis. What is the magnetic field at the centre P of the semiconductor loop?
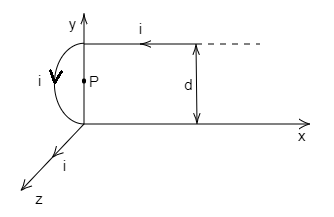
Solution
Hint
By using the formula of the magnetic field of a straight wire carrying the current, the magnetic field is determined. Here the current is passed in three wires, so the three magnetic fields are determined and by adding the three magnetic fields, the magnetic field at the centre P is determined.
The magnetic field of a straight wire carrying the current is given by,
⇒B=4πμ0r2I
Where, B is the magnetic field, μ0 is the permeability of free space, I is the current and r is the distance.
Complete step by step answer
The magnetic induction at P due to the current through straight part of the conductor parallel to x axis is, then
⇒B1=4πμ0r2I
The magnetic field act along z axis, then
⇒B1=4πμ0r2Ik^.................(1)
The magnetic field induction at P due to current through the semi-circular loop in x−y plane is, then
⇒B2=4πμ0r2Iπ
The magnetic field act along z axis, then
⇒B2=4πμ0r2Iπk^.................(2)
The magnetic field induction at P due to current through the straight part of the conductor coinciding with z axis is, then
⇒B3=4πμ0r2I
The magnetic act outwards, so it is negative, then
⇒B3=4πμ0r2I(−i^)..................(3)
The total magnetic field at P is,
⇒B=B1+B2+B3
By substituting the equation (1), equation (2) and equation (3) in the above equation, then the above equation is written as,
⇒B=(4πμ0r2Ik^)+(4πμ0r2Iπk^)+(4πμ0r2I(−i^))
By taking the term 4πμ0r2I as a common term and take this term outside from the equation, then the above equation is written as,
B=4πμ0r2I[k^+πk^−i^]
Then the above equation is also written as,
B=4πμ0r2I[(1+π)k^−i^]
Thus, the above equation shows the total magnetic field at the centre P.
Note
In every vector equation the unit vector is multiplied, so that the unit vector k^ is multiplied with the equation (1) and the equation (2) and the unit vector i^ is multiplied with the equation (3). The current is passing through the three wires, so the magnetic field is produced in both the three wires. By adding the three equations, the total magnetic field is determined.
