Question

An infinitely large thin plane sheet has an uniform surface charge density $+\sigma$. Obtain the expression for the amount of work done in bringing a point charge q from infinity to a point, distant r, in front of the plane charged sheet.

Answer 1

Hint: Knowledge of gauss law in electrostatics is necessary to solve this problem. Further, how the gauss law is used in different conditions, such as gauss law in the case of linear charge density, surface charge density and lastly in the case of volume charge density will be helpful too.

Complete step-by-step answer:
Let’s start by making a diagram for this problem.

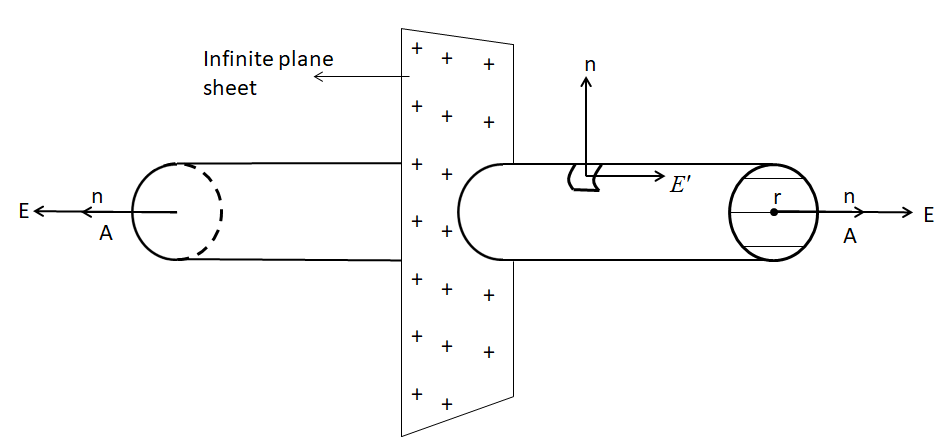
We have an infinitely large thin plane sheet having an uniform charge density $+\sigma$ throughout the surface. A charge is brought from infinity to a point at a distance r from the sheet. We will make a Gaussian surface as a cylinder of twice the same length from the sheet to the point passing through the sheet at the center of the cylinder.
The cross sectional area of the cylinder will be A.
Now let’s find out the Flux $'\phi '$ through the cylinder.
We know from gauss law: $\phi =\int{E.dS}$
Here, we have three surface area components. The 2 cross sectional area components, at the 2 opposite ends and the curved surface area components.
${{\phi }_{total}}={{\phi }_{cross\sec tion-1}}+{{\phi }_{cross\sec tion-2}}+{{\phi }_{curvedsurface}}$
Since, both the Electric field component and the area components will have the direction of outward normal. Hence, ${{\phi }_{cross\sec tion-1}}=\int{E.dA}$ and ${{\phi }_{cross\sec tion-2}}=\int{(-E).d{A}'}=\int{(-E).(-dA})=\int{E.dA}$
That is, the flux coming out of both the cross sectional areas are equal. Hence, when we calculate the net flux, they will add up.
Therefore, the net flux coming out of the cylinder will be, ${{\phi }_{total}}=2EA\cos {{0}^{0}}+EA\cos {{90}^{0}}$
$\Rightarrow {{\phi }_{total}}=2EA$
We also know that flux is equal to the net charge contained in the Gaussian surface. That is,$\phi =\dfrac{{{Q}_{enclosed}}}{{{\in }_{0}}}$
Since, we already have $\sigma$ surface charge density, hence, here the charge will be $\sigma .Area.$
Therefore, ${{\phi }_{total}}=\dfrac{{{Q}_{enclosed}}}{{{\in }_{0}}}\Rightarrow {{\phi }_{total}}=\dfrac{\sigma A}{{{\in }_{0}}}=2EA$
This implies, $E=\dfrac{\sigma }{2{{\in }_{0}}}$
Amount of work done ‘W’ to move a charge from infinity to a point is given by force ‘F’ times the displacement.
That is, $F=qE.$
Hence, the work done is, $dW=F.dr\Rightarrow W=-\int\limits_{\infty }^{r}{Fdr}$
$\therefore W=-\int\limits_{\infty }^{r}{\dfrac{\sigma q}{2{{\in }_{0}}}dr=}-\dfrac{\sigma q}{2{{\in }_{0}}}[r]_{\infty }^{r}=-\dfrac{\sigma qr}{2{{\in }_{0}}}$
However, the negative sign can be removed as it only states the direction of the work done.
Hence, the work done is, $W=\dfrac{\sigma qr}{2{{\in }_{0}}}$

Note: The reason why the Work done is negative is that $W=-\int\limits_{\infty }^{r}{F.dr}$, since the charge is initially brought from infinity to a point r. The distance is being reduced from the initial point to the final point. Hence, the negative sign is added. You may also say that displacement and force, both of which are vector quantities, are along the opposite directions.
In these kinds of vector quantities, negative signs only mean the direction with respect to another vector quantity.