Question

An infinite sequence of resistances is shown in the figure. The resultant resistance between A and B will be, when ${R_1} = 1\Omega$ and ${R_2} = 2\Omega$

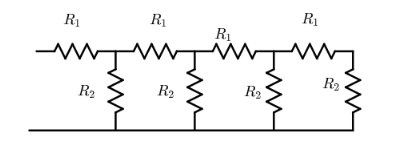
(A) Infinity
(B) $1\Omega$
(C) $2\Omega$
(D) $1.5\Omega$

Answer 1

The resistance is split in two parts by using symmetry and the resistance of single sections is calculated. It is assumed that the resistance of the rest of the figure is equivalent to a certain value. If we add one more branch, then the resultant resistance would be the same because this is an infinite sequence.

Complete step by step answer:
Let the resultant resistance be $R$ .
If we add one more branch, then the resultant resistance would be the same because this is an infinite sequence.
Now, we take the first segment from the given figure and evaluate separately. It is assumed that the resistance of the rest of the figure is equivalent to $R$ .
Now this resistance $R$ is connected in parallel to the resistance ${R_2}$ and ${R_2}$ resistor is in series with the resistor ${R_1}$ . The figure would then look somewhat like this.

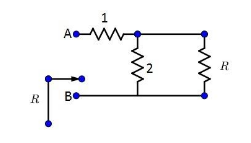
From the figure, it can be seen that, resistor ${R_1}$ is in series with the resistors ${R_2}$ and $R$ .
By laws of resistance addition,
${R_1}{R_2} + {R_1} = R$ .
$\Rightarrow 2R + R + 2 = {R^2} + R$ .
Simplifying this we get, ${R^2} - R - 2 = 0$ .
On factorising this equation, we get, $\left( {R - 2} \right)\left( {R + 1} \right) = 0$ .
We know that resistance value cannot be negative.
Thus,
$\left( {R - 2} \right) = 0$
$\Rightarrow R = 2\Omega$
Hence, the correct answer is Option C.

Note:
Whenever every resistance in a configuration is multiplied by a factor then the equivalent resistance also gets multiplied by that factor. Here, we split the resistance and also the series goes on to infinity which lets us make the necessary manipulations.
Steps involved have been listed below.
1. Split the resistance in two parts by using symmetry.
2. Calculate the resistance of a single section by using the fact mentioned above.
3. Going back to the original problem .Combine the resistances as they are in parallel.