Question
Question: An infinite number of charges, each of charge \(1\mu C\), are placed on the x-axis with coordinates ...
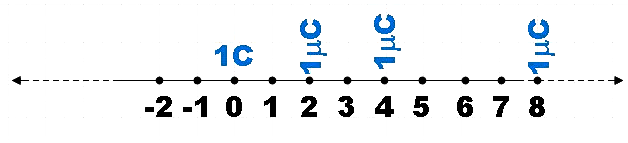
An infinite number of charges, each of charge 1μC, are placed on the x-axis with coordinates x=1, 2, 4, 8…∞ If a charge of 1C is kept at the origin, then what is the net force acting on 1C
A. 9000N
B. 12000N
C. 24000N
D. 36000N
Solution
As a first step, you could recall the coulomb’s law for two charges. Then you could apply the superposition principle for the system of charges. You could find a geometric progression as a result after taking the common terms out. Solving that you will get the force on the 1C charge at the origin.
Formula used:
Net force due to a system of charges,
Fnet=4πε01∑rij2qiqj
Complete Step by step solution:
In the question, we have a system of infinite number of charges each with a charge of 1μC. These charges are placed on the x-axis at coordinates x=1, 2, 4, 8…∞. We are asked to find the net force on a charge of magnitude 1C kept at origin due to the system of charges.
We know that the force between two charges is given by the Coulomb’s law which is given by,
F=4πε01r2q1q2
Now when we have a system of charges, the net force on a charge due to that system would be given by the sum of the forces due to each individual charge. This is called the superposition principle.
Therefore, the net charge would be given by,
Fnet=4πε01∑rij2qiqj
⇒Fnet=9×109×10−6(121+221+421+821+...) …………………………………. (1)
We see that, (121+221+421+821+...)is a geometric progression and its sum can be given by,
SUMGP=1−ra
Where, a is the first term and r is the common ratio.
r=141=41
So the sum of the GP would be,
SUMGP=1−411
⇒SUMGP=34 ………………………………………… (2)
Substituting (2) in equation (1), we get,
Fnet=9×109×10−6×34
∴Fnet=12000N
Therefore, we found the net force on the 1C charge placed at the origin due to the given system of charges would be 12000N.
Hence, option B is the correct answer.
Note:
While substituting the charges we have taken the common term outside which is 10−6C. While taking the sum of the geometric progression we mentioned a term common ratio. The common ratio is the ratio between two consecutive terms of a geometric progression. Also, the expression for the sum of GP is taken for progression with a common ratio that is less than 1 and more than -1 except 0.
